( ext{Description})
( ext{Solution})
有一个很强的转化:考虑构造 (s'=s[1]s[n]s[2]s[n-1]...s[frac{n}{2}]s[frac{n}{2}+1])。具体就感性理解吧:由于题目要求 (s_1=s_k,s_2=s_{k-1}...),可以知道分段后一定是对称的,所以反转就是要求 (s’) 的回文串分割次数(注意这里的回文是偶回文)。
显然有这样的转移:
其中 ([j+1,i]) 是一个偶回文串,这个可以用后缀自动机跳 (fa) 来维护。
考虑时间复杂度,其实这是 (mathcal O(n^2)) 的,数据是一个全为同种字符的串。
定义 ( ext{dif}(x)=s[x].len-s[s[x].fa].len),( ext{Block}(x)) 是 (x) 往上跳 (fa) 时第一个 ( ext{dif}) 不等于 ( ext{dif}(x)) 的节点。再令 (g[x]) 是 (x) 往上跳 (fa) 到 ( ext{Block}(x))(不包含 ( ext{Block}(x)))的节点的 (f)。
设 (x) 是加入 (i) 时的 (now)((now) 可以看看代码)。则 (g[x]) 就是 (f[i-s[x].len]+f[i-s[x].len+dif[x]]+f[i-s[x].len+dif[x] imes 2]+...+f[i-s[ ext{Block}(x)].len-dif[x]])。
这样搞的原因是使 (f[x]) 可以由 (f[s[x].fa]) 转移过来。
嫖了一张图(( ext{slink}) 就是 ( ext{Block})):
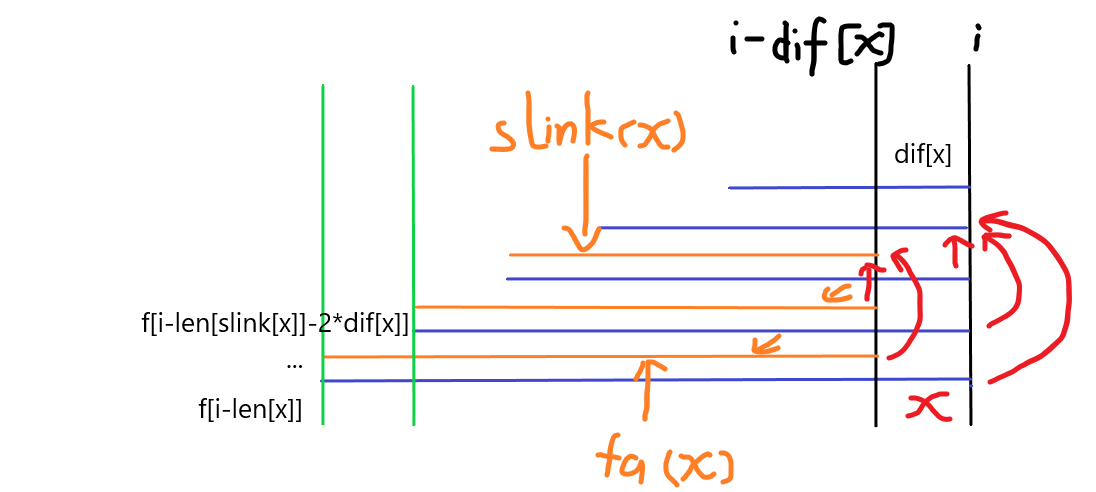
显然从下往上数第一条橙线就是从下往上数第二条蓝线(即 (s[x].fa))。橙线与其上面蓝线一一对应。
显然根据上面的定义,(s[x].fa) 未统计 ( ext{Block}(x)) 那条橙线,但 (x) 是能统计到 ( ext{Block}(x)) 下面那条蓝线的(显然橙线与下面一条蓝线贡献的 (f) 值一样)。
所以 (g[x]=g[s[x].fa]+f[i-s[ ext{Block}(x)].len- ext{dif}(x)])。
完了?还没呢!最重要的是,如何证明时间复杂度。
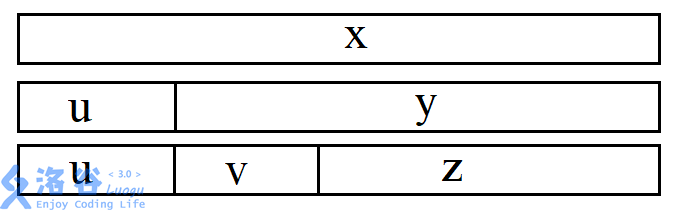
设 (x,y,z) 都是回文串并且 (y) 是 (x) 的最长回文后缀,(z) 是 (y) 的最长回文后缀。那么有:
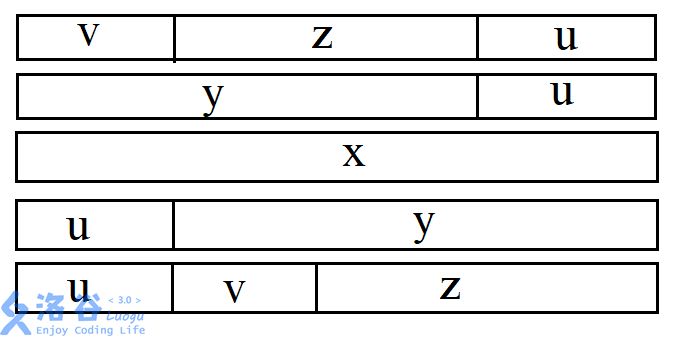
结论 1:如果 (u,v) 的长度相等,那么 (u,v) 是两个一模一样的字符串。
证明(约定 (a>b) 为长度比较):
- (u>y)。(v) 和 (u) 的长度不可能相等。
- (ule y)。(ule y)。由于 (x) 是回文串所以 (uy=yu) ,所以 (v) 是 (x) 的一个前缀,所以得证。
结论 2:不存在 (u<v) 的情况。
证明:
- (u>y)。显然。
- (ule y)。此时因为 (y) 是 (x) 的最长回文后缀,(z) 是 (y) 的最长回文后缀,那么 (u,v) 相对就是满足 (x,y) 最短的。将表中第二行与第四行对比,发现 (u) 移到第二行成为 (y) 的前缀后有中间那一部分是回文串((x) 是回文串,(u=u))。则 (u) 也可以满足 (y)。若 (u<v),(v) 就不是最小的了,矛盾。
结论 3:若 (u>v),则 (u>z)。
证明:
反证法。
假设 (z>u),且 (u>v)。
则 (z) 是 (zu) 的一个长度过半的公共前后缀。由于 (z) 是一个回文串,则此时 (zu) 是一个回文串(对比第一行和第五行)。又因为 (u>v),所以 (zu>y),且 (zu) 还是 (x) 的一个后缀,这与 (y) 是 (x) 的最长回文后缀的性质相矛盾。
回到原题,容易发现 (u=v) 时就是那一连串 ( ext{dif}) 相等的情况,当 (u>v) 就是遇到了 ( ext{Block}(x))。由 结论 3 得 (s[ ext{Block}(x)].len<frac{s[x].len}{2})!
所以每遇见 ( ext{Block}(x)) 就会使长度减半,我们最多会遇见 (log n) 个 ( ext{Block}(x))!
所以时间复杂度 (mathcal O(nlog n))。
( ext{Code})
#include <cstdio>
#define rep(i,_l,_r) for(register signed i=(_l),_end=(_r);i<=_end;++i)
#define fep(i,_l,_r) for(register signed i=(_l),_end=(_r);i>=_end;--i)
#define erep(i,u) for(signed i=head[u],v=to[i];i;i=nxt[i],v=to[i])
#define efep(i,u) for(signed i=Head[u],v=to[i];i;i=nxt[i],v=to[i])
#define print(x,y) write(x),putchar(y)
template <class T> inline T read(const T sample) {
T x=0; int f=1; char s;
while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
return x*f;
}
template <class T> inline void write(const T x) {
if(x<0) return (void) (putchar('-'),write(-x));
if(x>9) write(x/10);
putchar(x%10^48);
}
template <class T> inline T Max(const T x,const T y) {if(x>y) return x; return y;}
template <class T> inline T Min(const T x,const T y) {if(x<y) return x; return y;}
template <class T> inline T fab(const T x) {return x>0?x:-x;}
template <class T> inline T gcd(const T x,const T y) {return y?gcd(y,x%y):x;}
template <class T> inline T lcm(const T x,const T y) {return x/gcd(x,y)*y;}
#include <cstring>
const int mod=1e9+7,maxn=1e6+5;
char ori[maxn],str[maxn];
int n,g[maxn],f[maxn],len;
struct PAM {
int cnt,las;
struct node {
int fa,len,son[26],dif,Block;
} s[maxn];
PAM() {
s[0].len=0,s[1].len=-1;
s[0].fa=s[1].fa=1;
las=0,cnt=1;
}
int GetFail(int x) {
while(str[n-s[x].len-1]^str[n]) x=s[x].fa;
return x;
}
void Extend(int c) {
int cur=GetFail(las),now=s[cur].son[c];
if(!now) {
now=++cnt;
s[now].len=s[cur].len+2;
s[now].fa=s[GetFail(s[cur].fa)].son[c];
s[cur].son[c]=now;
s[now].dif=s[now].len-s[s[now].fa].len;
s[now].Block=(s[now].dif^s[s[now].fa].dif)?s[now].fa:s[s[now].fa].Block;
}
las=now;
}
void Update(int i) {
for(int p=las;p;p=s[p].Block) {
g[p]=f[i-s[s[p].Block].len-s[p].dif];
if(s[p].Block^s[p].fa) g[p]=(g[p]+g[s[p].fa])%mod; // 特判!!!
if(!(i&1)) f[i]=(f[i]+g[p])%mod;
}
}
} mc;
int main() {
scanf("%s",ori+1); len=strlen(ori+1);
rep(i,1,len>>1) str[(i<<1)-1]=ori[i];
rep(i,(len>>1)+1,len) str[(len-i+1)<<1]=ori[i];
f[0]=1;
rep(i,1,len) {
++n;
mc.Extend(str[i]-'a');
mc.Update(i);
}
print(f[n],'
');
return 0;
}