UVa 11168 (凸包+点到直线距离) Airport

题意：

平面上有n个点，求一条直线使得所有点都在直线的同一侧。并求这些点到直线的距离之和的最小值。

分析：

只要直线不穿过凸包，就满足第一个条件。要使距离和最小，那直线一定在凸包的边上。所以求出凸包以后，枚举每个边求出所有点到直线的距离之和得到最小值。

点到直线距离公式为：

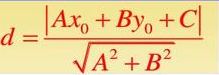
因为点都在直线同一侧，所以我们可以把加法“挪”到里面去，最后再求绝对值，所以可以预处理所有点的横坐标之和与纵坐标之和。当然常数C也要记得乘上n倍。

已知两点坐标求过该点直线的方程，这很好求不再赘述，考虑到直线没有斜率的情况，最终要把表达式中的分母乘过去。

//#define LOCAL
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;

struct Point
{
    double x, y;
    Point(double x=0, double y=0):x(x), y(y) {}
};
typedef Point Vector;
Point operator + (Point A, Point B)
{
    return Point(A.x+B.x, A.y+B.y);
}
Point operator - (Point A, Point B)
{
    return Point(A.x-B.x, A.y-B.y);
}
bool operator < (const Point& A, const Point& B)
{
    return A.x < B.x || (A.x == B.x && A.y < B.y);
}
bool operator == (const Point& A, const Point& B)
{
    return A.x == B.x && A.y == B.y;
}
double Cross(Vector A, Vector B)
{
    return A.x*B.y - A.y*B.x;
}

vector<Point> ConvexHull(vector<Point> p) {
  // 预处理，删除重复点
  sort(p.begin(), p.end());
  p.erase(unique(p.begin(), p.end()), p.end());

  int n = p.size();
  int m = 0;
  vector<Point> ch(n+1);
  for(int i = 0; i < n; i++) {
    while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
    ch[m++] = p[i];
  }
  int k = m;
  for(int i = n-2; i >= 0; i--) {
    while(m > k && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
    ch[m++] = p[i];
  }
  if(n > 1) m--;
  //for(int i = 0; i < m; ++i) printf("%lf %lf
", ch[i].x, ch[i].y);
  ch.resize(m);
  return ch;
}

double sumx, sumy;

double Dist(Point a, Point b, int m)
{
    double A = a.y-b.y, B = b.x-a.x, C = a.x*b.y - b.x*a.y;
    //printf("%lf %lf", fabs(A*sumx+B*sumy+C), sqrt(A*A+B*B));
    return (fabs(A*sumx+B*sumy+C*m) / sqrt(A*A+B*B));
}

int main(void)
{
    #ifdef LOCAL
        freopen("11168in.txt", "r", stdin);
    #endif
    
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; ++kase)
    {
        int n;
        vector<Point> p;
        sumx = 0.0, sumy = 0.0;
        scanf("%d", &n);
        for(int i = 0; i < n; ++i)
        {
            double x, y;
            scanf("%lf%lf", &x, &y);
            p.push_back(Point(x, y));
            sumx += x;    sumy += y;
        }
        vector<Point> ch = ConvexHull(p);
        int m = ch.size();
        //for(int i = 0; i < m; ++i)    printf("%lf %lf
", ch[i].x, ch[i].y);
        if(m <= 2)
        {
            printf("Case #%d: 0.000
", kase);
            continue;
        }
        
        double ans = 1e10;
        for(int i = 0; i < m; ++i)
            ans = min(ans, Dist(ch[i], ch[(i+1)%m], n));
        printf("Case #%d: %.3lf
", kase, ans/n);
    }
}