#1196 : 高斯消元·二
描述
在上一回中,小Hi和小Ho趁着便利店打折,买了一大堆零食。当他们结账后,看到便利店门口还有其他的活动。
店主:买了东西还可以参加游戏活动哦,如果能够完成游戏还有额外的奖品。
小Hi和小Ho赶紧凑了过去。
店主放了一块游戏板在店门口,有5行6列格子。左上角为坐标(1,1)。一部分格子是亮着的,另一部分是暗着的。

当按下某一个格子时,它和上下左右4个格子的状态就会改变。原来亮着的格子变成暗的,原来暗的格子会变亮。比如下图中按下标记有红叉的格子后,绿色虚线区域内的格子状态都会改变:
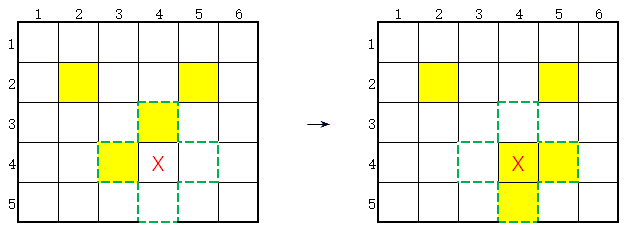
店主给出初始的状态,参加游戏的人员需要通过按下某些格子,让游戏板上所有的灯都亮起来就可以赢得奖品。
小Ho:这不就是开关灯问题么,看我来解决它!
提示:异或方程组
小Ho在游戏板上忙碌了30分钟,任然没有办法完成,于是他只好求助于小Hi。
小Ho:小Hi,这次又该怎么办呢?
小Hi:让我们来分析一下吧。
首先对于每一个格子的状态,可能会对它造成影响的是其自身和周围4个格子,这五个格子被按下的总次数也就等于该格子所改变的总次数。
对于任意一个格子,如果这个格子改变了偶数次状态,则等价于没有发生改变。
我们可以将1看作格子亮着,0看作格子暗着,每改变1次就加1,最后格子的状态等于其总数值 MOD 2。
则其运算结果刚好满足异或运算,即每改变一次等于状态值 xor 1。
同样的对于一个格子和它周围的4个格子来说,若格子被按下偶数次,它自身和周围4个格子的状态也等于没有发生改变。所以我们可以知道:任意一个格子至多被按下一次。
假设有数组x[1..30],分别表示这30个格子是否按下1次,若按下则x[i]=1,否则x[i]=0。
则对于1个格子,他最后的状态为:
当前状态 = 初始状态 xor (a[1] * x[1]) xor (a[2] * x[2]) xor ... xor (a[30] * x[30])
其中a[i]表示格子i是否会对当前格子产生影响,若能够则a[i] = 1,否则a[i] = 0
对方程进行变换有:
(a[1] * x[1]) xor (a[2] * x[2]) xor ... xor (a[30] * x[30]) = 当前状态 xor 初始状态
因为我们的目标是要让所有等格子都为亮的状态,故我们需要让 当前状态 = 1,则:
(a[1] * x[1]) xor (a[2] * x[2]) xor ... xor (a[30] * x[30]) = 1 xor 初始状态
不妨设y = 1 xor 初始状态:
(a[1] * x[1]) xor (a[2] * x[2]) xor ... xor (a[30] * x[30]) = y
对于所有的格子,我们可以连立出方程组:
(a[ 1][1] * x[1]) xor (a[ 1][2] * x[2]) xor ... xor (a[ 1][30] * x[30]) = y[ 1]
(a[ 2][1] * x[1]) xor (a[ 2][2] * x[2]) xor ... xor (a[ 2][30] * x[30]) = y[ 2]
...
(a[30][1] * x[1]) xor (a[30][2] * x[2]) xor ... xor (a[30][30] * x[30]) = y[30]
到此,我们的目标就是求出一个x[1..30],使得上面的方程组成立。
小Ho:这个看上去和高斯消元很像啊。
小Hi:没错,这个方程组叫异或方程组,它可以用和高斯消元同样的方法来解决。
其解答过程几乎和高斯消元无异,判定无解和多解的方式也相同。唯一需要注意的是消元过程不再是高斯消元的加减,而是通过xor运算来进行消元。比如消除第j行第i列的1:
a[j][k] = a[j][k] xor a[i][k], y[j] = y[j] xor y[i]
其原理是:
(a[j][1] * x[1]) xor (a[j][2] * x[2]) xor ... xor (a[j][30] * x[30]) xor (a[i][1] * x[1]) xor (a[i][2] * x[2]) xor ... xor (a[ i][30] * x[30]) = y[j] xor y[i] <=> ((a[j][1] * x[1]) xor (a[i][1] * x[1])) xor (((a[j][2] * x[2]) xor (a[i][2] * x[2]))) xor ... xor ((a[j][30] * x[30]) xor (a[i][30] * x[30])) = y[j] xor y[i]
<=> ((a[j][1] xor a[i][1]) * x[1]) xor ((a[j][2] xor a[i][2]) * x[2]) xor ... ((a[j][30] xor a[i][30]) * x[30]) = y[j] xor y[i]
而且由于给定游戏板是固定的,我们可以知道a[i][j]矩阵一定是固定的,而且通过计算可以知道我们消元得到的上三角矩阵也是固定的,并且在这一次的问题中该上三角矩阵是满秩的,所以其一定存在唯一解。
所以我们一定有办法完成这个游戏。
小Ho:我明白了,我这就去写程序,这奖品我拿定了!
输入
第1..5行:1个长度为6的字符串,表示该行的格子状态,1表示该格子是亮着的,0表示该格子是暗的。
保证一定存在解,且一定存在暗着的格子。
输出
需要按下的格子数量k,表示按下这k个位置后就可以将整个游戏板所有的格子都点亮。
接下来k行,每行一个坐标(x,y),表示需要按下格子(x,y)。x坐标较小的先输出,若x相同,则先输出y坐标较小的。
- 样例输入
-
001111 011111 111111 111110 111100
- 样例输出
-
2 1 1 5 6
分析:上面的提示说的很清楚,建一个30个未知数的方程组,
然后用高斯消元解方程,因为方程保证一定有解所以不用判断无解的情况。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int a[40][40]; int num[7][7]; int d[5][2]={0,1,0,-1,1,0,-1,0,0,0}; void Guass() { int N=30,M=31;//N行 for(int i=1;i<=N;i++)//计算上三角 { if(a[i][i]==0) { int k=N; for(;k>i;k--) if(a[k][i]!=0) break; swap(a[k],a[i]);//交换两行 } for(int k=i+1;k<=N;k++) { if(a[k][i]==0) continue;//这里要判断一下 for(int j=i+1;j<=M;j++) a[k][j]=a[k][j]^a[i][j]; a[k][i]=0; } } //从下往上消去 int ans=0; for(int i=N;i;i--) { for(int k=i-1;k;k--) { if(a[k][i]==0) continue;//这里要判断一下 a[k][M]=a[k][M]^a[i][M]; a[k][i]=0; } } } int main() { int cnt=1,x; for(int i=1;i<=5;i++) for(int j=1;j<=6;j++) { scanf("%1d",&x); a[cnt][31]=1^x;//当前状态^最终状态 num[i][j]=cnt++; } for(int i=1;i<=5;i++) { for(int j=1;j<=6;j++) { int t=num[i][j];//第t行 for(int k=0;k<5;k++) a[t][num[i+d[k][0]][j+d[k][1]]]=1; } } Guass(); int ans=0; for(int i=1;i<=30;i++) if(a[i][31]) ans++; printf("%d ",ans); for(int i=1;i<=30;i++) { if(a[i][31]==0) continue; printf("%d %d ",(i-1)/6+1,(i-1)%6+1); } return 0; }
