这大概是唯一一道小C重写了4次的题目。
姿势不对的树套树(Fail) → 分块(Fail) → 整体二分(Succeed) → 树套树(Succeed)。
让小C写点心得静静。
Description
有N个位置,M个操作。操作有两种,每次操作如果是1 a b c的形式表示在第a个位置到第b个位置,每个位置加入一个数c。如果是2 a b c形式,表示询问从第a个位置到第b个位置,第C大的数是多少。
Input
第一行N,M。
接下来M行,每行形如1 a b c或2 a b c。
Output
输出每个询问的结果
Sample Input
2 5
1 1 2 1
1 1 2 2
2 1 1 2
2 1 1 1
2 1 2 3
Sample Output
1
2
1
HINT
N,M<=50000,N,M<=50000
a<=b<=N
1操作中abs(c)<=N
2操作中c<=Maxlongint
Solution
这道题让小C见识了整体二分的妙用,它是一种离线做法。
整体二分的思想就是二分答案。以单次询问的区间K大为例,我们可以二分答案,通过统计比当前二分出的答案大的数的个数,与K比较,决定缩小或是增大答案。
而对于多次询问,我们整体二分所有询问的答案,对于每个询问,我们都通过比较,来决定它们应该进入小的那一半,还是大的那一半。
而对于每个修改,我们也要判断它会对哪个区间的答案产生影响,来决定它应该进入哪一半。
要注意,任何时候,每个询问和修改之间的相对顺序都不能变。
这样的时间复杂度为什么是科学的呢?我们脑补一下:
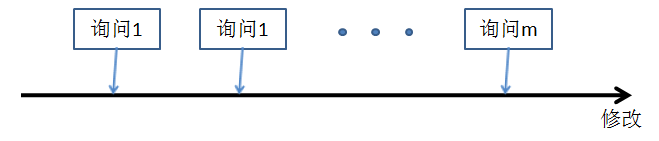
动态询问的本质就是边修改边询问的过程,对于每次修改,我们用数据结构维护要统计的信息。(这是一句废话)
因为有数据结构的存在,时间复杂度才是科学的。(还不理解的读者请将这一行无视,继续往下看)
What?还需要数据结构?那我要整体二分何用?我咋不大力树套树呢?
整体二分当然不是白写的。原来树套树要维护的是,值域区间[L,R]内,数组的信息,需要二维。
而整体二分时,我们只需要维护 当前 二分的值域区间[L,R]内,数组的信息,只需要一维。
因为做完 当前 这段值域区间内的事情后,这棵线段树/平衡树就彻底没用了,因为关于它的所有事情都做完了,清空就行。(理解了再往下看吧)
这就巧妙利用离线做法将数据结构降维,空间和时间(常数)上都有很大的提升。
最后证明一下时间复杂度:对于每个询问和修改,我们都在二分答案的 log 个区间内做了一遍,总时间复杂度。
当然具体实现还有一些细节,还不理解的可以参见小C的代码。
说说这道题的题解:
树套树:以值域为第一维,以数组下标为第二维,第二维维护区间和。对于每个询问,像二分答案一样在第一维上走到底。
整体二分:离线,把树套树做法降维。
整体二分:
#include <cstdio> #include <cstring> #include <algorithm> #define l(a) son[a][0] #define r(a) son[a][1] #define MN 50005 #define ll long long using namespace std; struct meg{int g,x,y,z,pos,gs;}q[MN],q1[MN],q2[MN]; int son[MN<<2][2],tg[MN<<2],din,rt; int ans[MN],n,m,ain; ll t[MN<<2]; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } inline void mark(int &x,int L,int R,int z) { if (!x) {x=++din; l(x)=r(x)=t[x]=tg[x]=0;} t[x]+=1LL*z*(R-L+1); tg[x]+=z; } inline void down(int x,int L,int R) { if (!tg[x]) return; int mid=L+R>>1; mark(l(x),L,mid,tg[x]); mark(r(x),mid+1,R,tg[x]); tg[x]=0; } ll getsum(int x,int L,int R,int ql,int qr) { if (!x) return 0; if (ql==L&&qr==R) return t[x]; down(x,L,R); int mid=L+R>>1; if (qr<=mid) return getsum(l(x),L,mid,ql,qr); else if (ql>mid) return getsum(r(x),mid+1,R,ql,qr); else return getsum(l(x),L,mid,ql,mid)+getsum(r(x),mid+1,R,mid+1,qr); } void add(int &x,int L,int R,int ql,int qr) { if (!x) {x=++din; l(x)=r(x)=t[x]=tg[x]=0;} if (ql==L&&qr==R) {mark(x,ql,qr,1); return;} down(x,L,R); int mid=L+R>>1; if (qr<=mid) add(l(x),L,mid,ql,qr); else if (ql>mid) add(r(x),mid+1,R,ql,qr); else add(l(x),L,mid,ql,mid),add(r(x),mid+1,R,mid+1,qr); t[x]=t[l(x)]+t[r(x)]; } void work(int L,int R,int hd,int tl) { if (hd>tl) return; register int i; if (L==R) {for (i=hd;i<=tl;++i) if (q[i].g==2) ans[q[i].pos]=L; return;} int mid=L+R>>1,p1=0,p2=0; ll lt; rt=din=0; for (i=hd;i<=tl;++i) { if (q[i].g==1) { if (q[i].z>mid) add(rt,1,n,q[i].x,q[i].y),q2[++p2]=q[i]; else q1[++p1]=q[i]; } else if (q[i].g==2) { lt=getsum(rt,1,n,q[i].x,q[i].y); if (lt+q[i].gs>=q[i].z) q2[++p2]=q[i]; else q[i].gs+=lt,q1[++p1]=q[i]; } } for (i=1;i<=p1;++i) q[hd+i-1]=q1[i]; for (i=1;i<=p2;++i) q[hd+p1+i-1]=q2[i]; work(L,mid,hd,hd+p1-1); work(mid+1,R,hd+p1,tl); } int main() { register int i; n=read(); m=read(); for (i=1;i<=m;++i) {q[i].g=read(); q[i].x=read(); q[i].y=read(); q[i].z=read(); if (q[i].g==2) q[i].pos=++ain;} work(-n,n,1,m); for (i=1;i<=ain;++i) printf("%d ",ans[i]); }
树套树:
#include <cstdio> #include <cstring> #include <algorithm> #define l(a) (a<<1) #define r(a) (a<<1|1) #define L(a) (son[a][0]) #define R(a) (son[a][1]) #define TMN 15000005 #define MN 50005 #define ll long long using namespace std; ll t[TMN]; int son[TMN][2],tg[TMN],rt[MN<<3],din; int n,m; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } ll Tgetsum(int x,int L,int R,int ql,int qr) { if (!x) return 0; if (ql==L&&qr==R) return t[x]; int mid=L+R>>1; ll lt=1LL*tg[x]*(qr-ql+1); if (qr<=mid) return lt+Tgetsum(L(x),L,mid,ql,qr); else if (ql>mid) return lt+Tgetsum(R(x),mid+1,R,ql,qr); else return lt+Tgetsum(L(x),L,mid,ql,mid)+Tgetsum(R(x),mid+1,R,mid+1,qr); } void Tadd(int &x,int L,int R,int ql,int qr) { if (!x) x=++din; if (ql==L&&qr==R) {++tg[x]; t[x]+=(ll)R-L+1; return;} int mid=L+R>>1; if (qr<=mid) Tadd(L(x),L,mid,ql,qr); else if (ql>mid) Tadd(R(x),mid+1,R,ql,qr); else Tadd(L(x),L,mid,ql,mid),Tadd(R(x),mid+1,R,mid+1,qr); t[x]=t[L(x)]+t[R(x)]+1LL*tg[x]*(R-L+1); } int getk(int x,int L,int R,int z,int yl,int yr) { if (L==R) return L; ll lt; int mid=L+R>>1; if ((lt=Tgetsum(rt[r(x)],1,n,yl,yr))<z) return getk(l(x),L,mid,z-lt,yl,yr); else return getk(r(x),mid+1,R,z,yl,yr); } void add(int x,int L,int R,int q,int yl,int yr) { Tadd(rt[x],1,n,yl,yr); if (L==R) return; int mid=L+R>>1; if (q<=mid) add(l(x),L,mid,q,yl,yr); else add(r(x),mid+1,R,q,yl,yr); } int main() { register int g,x,y,z; n=read(); m=read(); while (m--) { g=read(); x=read(); y=read(); z=read(); if (g==1) add(1,-n,n,z,x,y); else if (g==2) printf("%d ",getk(1,-n,n,z,x,y)); } }
Last Word
说说前两次打这题的惨痛经历吧:
第一次树套树把(相对于正解)第一维和第二维搞反了,导致空间爆炸。
第二次分块,脑补了一个时间和空间都是O(n*sqrt(n)*log(n))的做法(权值线段树+替罪羊树瞎写),空间还是爆炸。
两次做法的思路都是二分答案,而且都把数组下标看作是第一维。
不过所幸打的这几次都没怎么需要Debug。打得挺爽。