Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.
Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
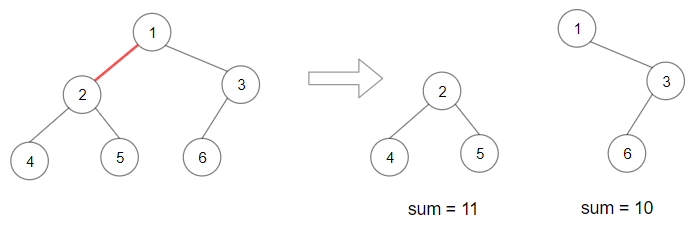
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Example 2:
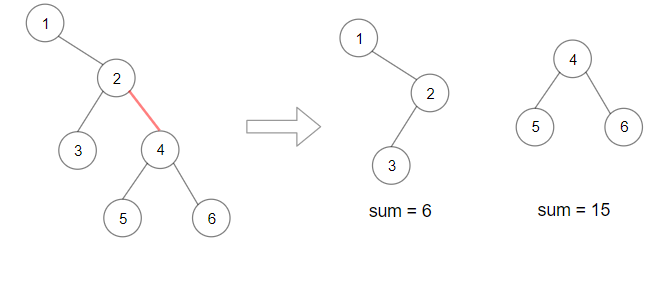
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Example 3:
Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025
Example 4:
Input: root = [1,1]
Output: 1
Constraints:
- Each tree has at most
50000nodes and at least2nodes. - Each node's value is between
[1, 10000].
题意给了一棵树,让将这棵树分成两棵子树,使得两棵子树的结点的和乘积最大,并求这个乘积。题目中所说的至少两个结点说的给的那棵树至少有两个结点,而不是每棵子树都要有两个结点,这点一开始没明白。。。
这个题初看不知道如何下手,我们抓住关键点,子树的和。那么我们第一步可以写出一个求一棵树的结点的和的函数。
private int getSum(TreeNode root) {
if (root == null) {
return 0;
}
int res = (root.val + getSum(root.left) + getSum(root.right)) % mod;
return res;
}
那么我们现在要做的就是以什么样的策略将这棵树分成两个子树求积。一开始想到了累加和的策略,但是不知道如何实现,在网上找了很久找到了。附上代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int mod = 1000000007;
List<Integer> sums = new ArrayList<>();
public int maxProduct(TreeNode root) {
if (root == null) {
return 0;
}
int all = getSum(root);
long ret = 0;
for (int v : sums) {
ret = Math.max(ret, (long)v * (all - v));
}
return (int)(ret % mod);
}
private int getSum(TreeNode root) {
if (root == null) {
return 0;
}
int res = (root.val + getSum(root.left) + getSum(root.right)) % mod;
sums.add(res);
return res;
}
}
这里相当于一开始就以后续遍历的方式,将以每一个结点为根结点的子树的和append到了sums中。
最后遍历一遍sums这个列表计算即可。