畅通工程续（Dijkstra算法）

推荐一篇很好的文章 ：如夜_YanBaoC。

我在这里就只是谈谈自己对Dijkstra算法的理解了。

 首先，我们需要知道DIjkstra算法是解决哪类问题的——对于单源点出发，到达某一点的最短距离。那适用于什么条件呢？——权重值为正的无向，有向连通图。（可以解负权的吗？这个问题先放放，我们后面再讲）

我们先来看看一个图

假设我们从0位置到5位置；

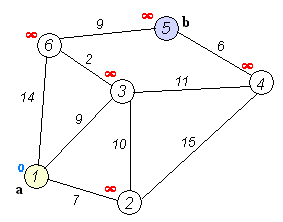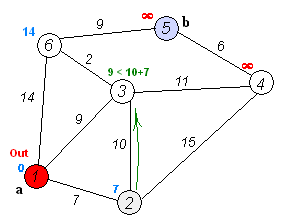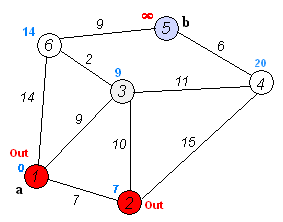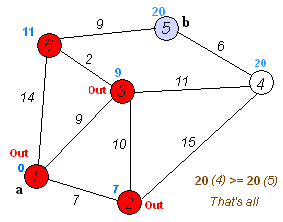
第一步：我在这个用map[start-->end]，start起始驱节点，end下一驱节点。map[1-->2]=7，map[1-->3]=9, map[1-->6]=14,所以min(7,9,14)=7。改变驱节点为2。

第二步：从2驱节点开始，有3,4，可以连接。但我们前驱节点1也可以和3相连，所以一样需要比较。

　　　　map[2-->3]=17,map[2-->4]=22,map[1-->3]=9.所以min(17,22.9)=9，改变驱节点为3。

第三步:   从3驱节点开始，有6,4可接，故map[3-->6]=11,map[3-->4]=20,map[1-->6]=14，所以min(11,20,14)=11.改变驱节点为6。

第三步：从6节点开始，直接到5 就完成了。 但我们发现，还要一条路，可以走和它一样的路数，那我们的代码是否会执行呢？

这就是Dijkstra算法的大致流程了。那怎么代码予以实现呢？我接下来给出该算法的模板（以此题为模板）：

1.我们要把地图绘制出来，我们要清楚的知道从某一点到某一点的距离，其实很简单。

　　G【】【】地图数组，dis【】记录从起始驱节点到任意点的距离。

     for(i=0;i<n;i++)//n代表点的个数。
            for(j=0;j<n;j++)
                G[i][j] = i==j?0:MAX;//MAX无穷大。
      while(m--)
      {
            scanf("%d %d %d",&u,&v,&w);
            if(G[u][v]>w)
                G[u][v] = G[v][u] = w;
      }

2.核心代码：

void dijkstra()
{
    bool vis[203];// 标记该点是否访问过。
    int dis[203];//保存最短路径。
    int i, j, k;

    for(i=0;i<n;i++)
        dis[i] = G[s][i];//记录各个点的距离
    memset(vis,false,sizeof(vis));//初始化为假 表示未访问过
    dis[s] = 0;//起始点距离为0
    vis[s] = true;//起始点点访问过了，标记为真
    for(i=1;i<n;i++)//G.V-1次操作+上面对s的访问 = G.V次操作
    {
        k = -1;
        for(j=0;j<n;j++)//从尚未访问过的点中选一个距离最小的点
            if(!vis[j] && (k==-1||dis[k]>dis[j]))//未访问过 && 是距离最小的
                k = j;
        if(k == -1)//若图是不连通的则提前结束
            break;//跳出循环
        vis[k] = true;//将k点标记为访问过了
        for(j=0;j<n;j++)//松弛操作
            if(!vis[j] && dis[j]>dis[k]+G[k][j])//该点为访问过 && 可以进行松弛
                dis[j] = dis[k]+G[k][j];//j点的距离  大于当前点的距离+w(k,j) 则松弛成功，进行更新
    }
    printf("%d
",dis[t]==MAX?-1:dis[t]);//输出结果
}