「联赛模拟测试12」sum 部分分详解

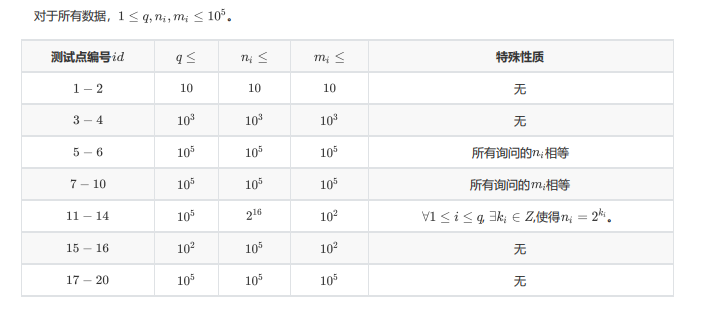
打表好题

1.部分分1（1~4）

观察到(n)，(m)很小，可以杨辉三角(n^2)预处理每一个组合数，询问时直接累加

      if(id<=4){
		cc[1][1]=cc[1][0]=1;
		for(int i=2;i<=10;i++){
			cc[i][0]=cc[i-1][0]=1;
			for(int j=1;j<=10;j++){
				cc[i][j]=(cc[i-1][j]+cc[i-1][j-1])%mol;
			}
		}
		int q=read();
		for(int i=1;i<=q;i++){
			n=read(),m=read();ans=0;
			for(int j=0;j<=m;j++)ans=(ans+cc[n][j])%mol;
			printf("%lld
",ans);
		}
	}

2.部分分2（5~6）

(n)都相同，直接(nlogn)预处理(n)的每一个组合数，然后累加，(O(1))询问

      if(id<=6){
		int q=read(),maxm=0;
		for(int i=1;i<=q;i++){
			qn[i]=read(),qm[i]=read();
			maxm=max(maxm,qm[i]);
		}
		Init();
		sum[0]=b[0]=1;
		for(int i=1;i<=maxm;i++)b[i]=C(qn[1],i),sum[i]=(sum[i-1]+b[i])%mol;
		for(int i=1;i<=q;i++){
			printf("%lld
",sum[qm[i]]);
		}
	}

3.部分分3（11~16）

观察下表：

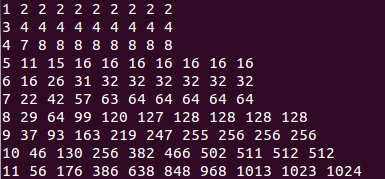
发现(f_{i,j}=f_{i-1,j-1}+f_{i-1,j})
100*100000，显然能跑过

      if(id<=16){
		int q=read();
		for(int i=1;i<=maxs/2;i++)f[i][i]=qpow(2,i),f[0][i]=1;
		for(int i=1;i<=10;i++){
			f[i-1][1]=i;f[i][0]=1;
			for(int j=1;j<=10;j++){
				f[i][j]=(1LL*f[i-1][j]+f[i-1][j-1])%mol;
				//cout<<f[i][j]<<" ";
			}
			//puts("");
		}
		for(int i=1;i<=q;i++){
			n=read(),m=read();
			printf("%lld
",f[n][m]);
		}
	}

4.部分分4（7~8）

(m)都相同，有点难找，所以放在了最后
由上表，观察每一列(以第五列为例)
(120=63*2-6)
(219=120*2-21)
(382=219*2-56)
貌似是组合，再结合杨辉三角的表，发现后面那数是斜着的杨辉三角，即(C(_6^5),C(_7^5),C(_8^5))
得出柿子：(f_{i,j}=2 imes f_{i-1,j}-C(_{i-1}^j))

       if(id<=10){
		int q=read();Init();
		for(int i=1;i<=q;i++)qn[i]=read(),qm[i]=read();
		for(int i=0;i<=qm[1];i++)sum[i]=qpow(2,i);
		for(int i=qm[1]+1;i<=maxs/2;i++)sum[i]=(2LL*sum[i-1]%mol-C(i-1,i-qm[1]-1)+mol)%mol;
		for(int i=1;i<=q;i++)cout<<sum[qn[i]]<<endl;
	}

5.部分分5(17~20)

发现，(f_{i,j})转移到(f_{i-1,j})(f_{i,j-1})的柿子都有，加上可以离线，所以直接莫队，以(i)为第一关键字，(j)为第二关键字，然后就裸的莫队（然而谁想的到会用莫队）

      int p=read();Init();n=1e5;
		for(register int i=1;i<=p;i++)q[i].x=read(),q[i].y=read(),q[i].id=i,q[i].belong=((q[i].x-1)/sqrt(n)/2)+1;
		sort(q+1,q+1+p);
		int nowl=1,nowr=0;ans=1;
		for(register int i=1;i<=p;i++){
			while(nowl<q[i].x)nowl++,ans=(ans*2LL%mol-C(nowl-1,nowl-nowr-1)+mol)%mol;
			while(nowr<q[i].y)nowr++,ans=(ans+C(nowl,nowr))%mol;
			while(nowr>q[i].y)ans=(ans-C(nowl,nowr)+mol)%mol,nowr--;
			while(nowl>q[i].x)ans=(ans+C(nowl-1,nowl-nowr-1))%mol*ny[2]%mol,nowl--;
			anss[q[i].id]=ans;
			//cout<<nowl<<" "<<nowr<<" "<<ans<<endl;
		}
		for(register int i=1;i<=p;i++)cout<<anss[i]<<endl;