顺序表
在程序中,经常需要将一组(通常是同为某个类型的)数据元素作为整体管理和使用,需要创建这种元素 组,用变量记录它们,传进传出函数等。一组数据中包含的元素个数可能发生变化(可以增加或删除元 素)。 对于这种需求,最简单的解决方案便是将这样一组元素看成一个序列,用元素在序列里的位置和顺序,表示 实际应用中的某种有意义的信息,或者表示数据之间的某种关系。 这样的一组序列元素的组织形式,我们可以将其抽象为线性表。一个线性表是某类元素的一个集合,还记录 着元素之间的一种顺序关系。线性表是最基本的数据结构之一,在实际程序中应用非常广泛,它还经常被用 作更复杂的数据结构的实现基础。 根据线性表的实际存储方式,分为两种实现模型: ·顺序表,将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由它们的存储顺序自然表示
注意:数组和python中的列表有些不同的地方 比如说存储的数据类型 数据长度 ·链表,将元素存放在通过链接构造起来的一系列存储块中。
顺序表的基本形式

图a表示的是顺序表的基本形式,数据元素本身连续存储,每个元素所占的存储w元大小固定相同,元素的 下标是其逻辑地址,而元素存储的物理地址(实际内存地址)可以通过存储区的起始地址Loc(eo)加上逻辑 地址(第个元素)与存储单元大小(c)的乘积计算而得,即: Loc(ei)=Loc(eo)+c*i 故,访问指定元素时无需从头遍历,通过计算便可获得对应地址,其时间复杂度为0(1)。 如果元素的大小不统一,则须采用图b的元素外置的形式,将实际数据元素另行存储,而顺序表中各单元位 置保存对应元素的地址信息(即链接)。由于每个链接所需的存储量相同,通过上述公式,可以计算出元素 链接的存储位置,而后顺着链接找到实际存储的数据元素。注意,图b中的c不再是数据元素的大小,而是存 储一个链接地址所需的存储量,这个量通常很小 图b这样的顺序表也被称为对实际数据的索引,这是最简单的索引结构。
顺序表的操作
增加元素
如图所示,为顺序表增加新元素111的三种方式
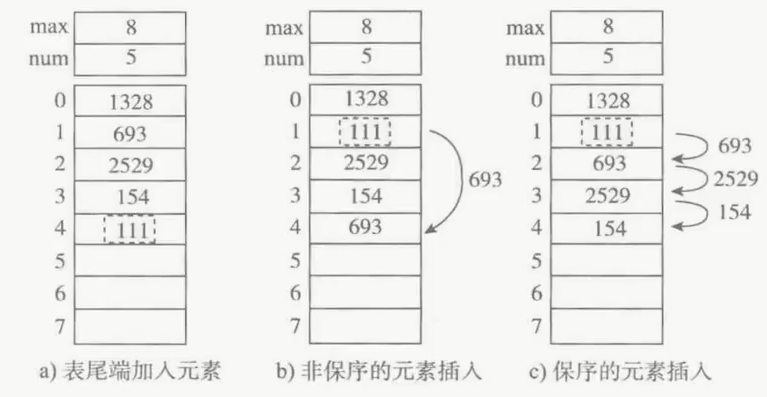
a.尾端加入元素,时间复杂度为O(1) b.非保序的加入元素(不常见),时间复杂度为0(1) c.保序的元素加入,时间复杂度为O(n)
删除元素

a.删除表尾元素,时间复杂度为O(1) b.非保序的元素删除(不常见),时间复杂度为0(1) c.保序的元素删除,时间复杂度为O(n)
Python中的顺序表
Python中的list和tuple两种类型采用了顺序表的实现技术,具有前面讨论的顺序表的所有性质。 tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态的任何操作,而其他方面,则与list的性 质类似。
list的基本实现技术
Python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作中维持已有元素的
顺序(即保序),而且还具有以下行为特征:
·基于下标(位置)的高效元素访问和更新,时间复杂度应该是0(1);
为满足该特征,应该采用顺序表技术,表中元素保存在一块连续的存储区中。
·允许任意加入元素,而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变。
为满足该特征,就必须能更换元素存储区,并且为保证更换存储区时list对象的标识id不变,只能采用分
离式实现技术。
在Python的官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x) (或list.insert(len(list),x),即尾部插入)比在指定位置插入元素效率高的原因。 在Python的官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x) (或list.insert(len(list)),x),即尾部插入)比在指定位置插入元素效率高的原因。 在Python的官方实现中,list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳 8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但 如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方 式,是为了避免出现过多空闲的存储位置。
顺序表的结构与实现
顺序表的结构

顺序表的两种基本实现方式
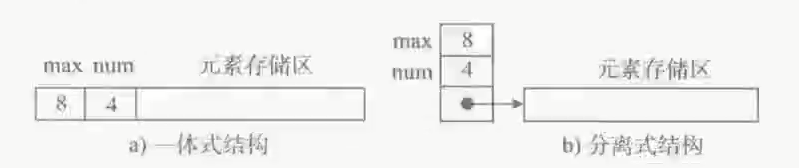
图a为一体式结构,存储表信息的单元与元素存储区以连续的方式安排在一块存储区里,两部分数据的整体 形成一个完整的顺序表对象。 一体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的一部分,顺序表创建后,元素存储 区就固定了。 图b为分离式结构,表对象里只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另一 个独立的元素存储区里,通过链接与基本表对象关联。
元素存储区替换
一体式结构由于顺序表信息区与数据区连续存储在一起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了。 分离式结构若想更换数据区,只需将表信息区中的数据区链接地址更新即可,而该顺序表对象不变。
元素存储区扩充
采用分离式结构的顺序表,若将数据区更换为存储空间更大的区域,则可以在不改变表对象的前提下对其数 据存储区进行了扩充,所有使用这个表的地方都不必修改。只要程序的运行环境(计算机系统)还有空闲存 储,这种表结构就不会因为满了而导致操作无法进行。人们把采用这种技术实现的顺序表称为动态顺序表, 因为其容量可以在使用中动态变化。
扩充的两种策略
每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。 特点:节省空间,但是扩充操作频繁,操作次数多。 每次扩充容量加倍,如每次扩充增加一倍存储空间。 特点:减少了扩充操作的执行次数,但可能会浪费空间资源。以空间换时间,推荐的方式。