周博磊老师强化学习纲领笔记第一课：强化学习基础

第一课：强化学习智能体的主要组成部分：

• Policy：引导智能体如何选取动作
• Value function：来判断每个状态或者动作的好坏
• Model：智能体在环境中的状态表示

Policy

• 一个决策就是智能体选取动作的模型
• 一个决策是一个映射函数，从状态、或者观测值到动作的映射
• 随机决策：随机概率 (pi(a|s)=P[A_t=a|S_t=s])
• 确定策略：(a^*=argmax_api(a|s))

Value function

• 价值函数：期望发现一个未来总收益的和是最大的(pi)策略
• 即时收益，和未来总收益，折扣因子
• (G_t=sum_{k=0}^{infty}gamma^kR_{t+k+1})，(G_t)代表未来总收益
• 用来量化状态和动作的好坏， (v_pi(s)=mathbb{E}_pi[G_t|S_t=s]=mathbb{E}_pi[sum_{k=0}^{infty}gamma^kR_{t+k+1}|S_t=s],\,for\, all \,sin S)，在状态(s)下的总收益是(v_pi(s))。
• Q函数（用来在动作空间中选择动作），(q_pi(s,a)=mathbb{E}_pi[G_t|S_t=s,A_t=a]=mathbb{E}_pi[sum_{k=0}^{infty}gamma^kR_{t+k+1}|S_t=s,A_t=a])，在状态为(s)，动作为(a)的时候价值是(q_pi(s,a))。

Model

• 模型所要预测的就是环境接下来就怎么变化
• 预测下一个状态：(P^a_{ss'}=mathbb{P}[S_{t+1}=s'|S_t=s,A_t=a])，在状态为(s)的时候采取动作(a)，状态幻化成(s')的概率为(P^a_{ss'})
• 预测下一个奖励回报：(R_s^a=mathbb{E}[R_{t+1}|S_t=s,A_t=a])，在状态为(s)的时候采取动作(a)的下一个奖励回报的值为(R_s^a)

马尔可夫决策

• (P^a)是每个动作的转换模型，(P(S_{t+1}=s'|S_t=s,A_t=a))
• (R)是回报函数(R(S_t=s,A_t=a)=mathbb{E}[R_t|S_t=s,A_t=a])
• 折扣因子(gamma in [0,1])，一般采用这几个折扣因子0.95, 0.98, 0.99, 0.995

Value-based agent，Policy-based agent和Actor-Critic agent

• Value-based agent：有明确的价值函数，没有决策函数，但是决策函数可以通过价值函数来得到
• Policy-based agent：没有价值函数，只有决策函数
• Actor-Critic agent：既有价值函数，又有决策函数

Model-based和Model-free

• Model-based：有明确的模型，也许有，也许没有价值和决策函数
• Model-free：有价值函数或者决策函数，没有模型

第二课：MDP：马尔可夫决策过程：

为什么要用折扣因子(gamma)

• 有些马尔可夫链是带环的，使用折扣因子是为了避免无穷的奖励
• 将未来的不确定性能够表示出来
• 对于一些有价值的奖励，希望能够即刻的得到奖励，而不是在以后得到奖励
• 人的行为也是更喜欢得到即刻奖励
• (gamma)设为0的话：只在乎即刻奖励，(gamma)设为1的话：未来奖励和即刻奖励权重相等。

求价值函数的方法，迭代的方法，用来求解状态比较多的环境

• 动态规划

利用贝尔曼公式，(Q^π(s,a)=r+γQ^π(s′,π(s' ))) ,采用迭代的方法，逐渐的更新每个状态的价值，当价值变化不大的时候，就停止更新。

• 蒙特卡洛随机采样

例如求(V(s_4))，从(s_4)开始随机产生很多的轨迹，然后每个轨迹算得它的奖励，然后所有的奖励再取一个平均

• 时序差分学习（动态规划+蒙特卡洛）

Policy evaluation on MDP

• 当我们给定好一个MDP的时候，我们有一个事先定义好的policy (pi)，根据当前的这个policy (pi) 我们可以获得到多大的价值。

• Bellman expectation backup :

  [v_{t+1}(s)=sum_{a in A}pi(a|s)[R(s,a)+gammasum_{s' in S}P(s'|s,a)v_t(s')] ag 1 ]

当前状态(s)的(（t+1）)步价值（通过迭代的方式不断地更新当前状态的价值，也就是从第(t)步价值来求得第(（t+1）)步的价值）就等于，在当前状态下，所有可能发生的动作(a)，在当前状态(s)下执行动作(a)的概率乘当前状态(s)下执行动作(a)的回报(R(s,a))，再加上在当前状态(s)下执行动作(a)的概率乘衰减因子，再乘上在状态(s)下执行动作(a)，到达状态(s')的概率，再乘上在状态(s')下的价值。

• 马尔可夫奖励过程与马尔可夫决策过程的差别就是，马尔可夫奖励过程不考虑动作action，(MRP<S,P^{pi},R,gamma>)

[v_{t+1}(s)=R^pi(s)+gamma P^pi(s'|s)v_t(s') ag 2 ]

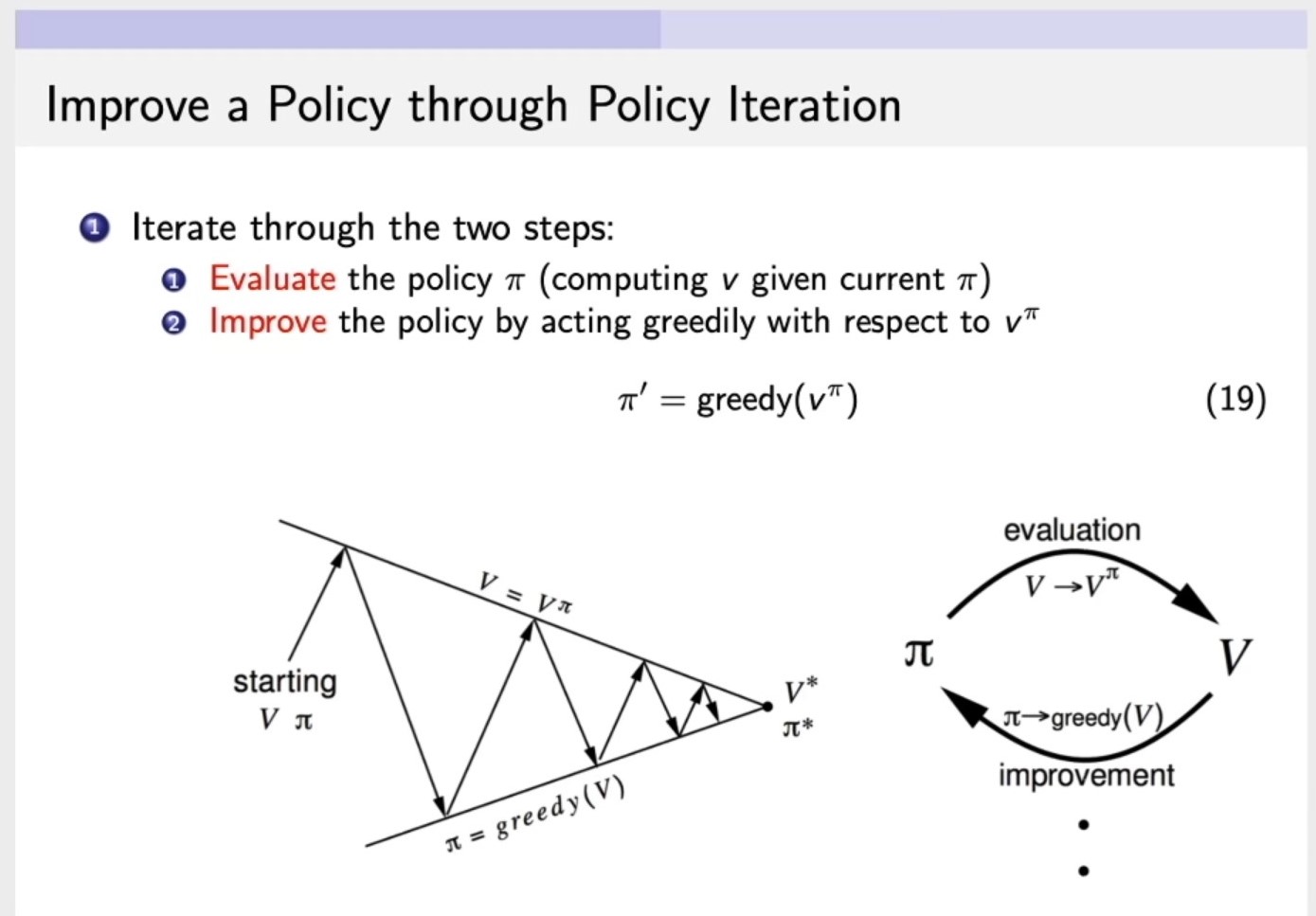
Improve a Policy through Policy Iteration

• Iterate through the two steps:
  • Evaluate the policy (pi) (computing (v) given current (pi))，第一步：计算v函数，输入，环境，策略以及衰减因子，来计算这个策略的价值。
  • Improve the policy by acting greedily wirh respect to (v^pi)，第二步：改进策略policy，通过对 (v^pi) （第一步通过(pi)求解出来的(v)）采取贪心的算法，来改进策略policy。