20172326 《程序设计与数据结构》第六周学习总结

学号 20172326 《程序设计与数据结构》第六周学习总结

教材学习内容总结

非线性数据结构——树

• 结点：结点分为根节点，内部结点。根据结点分为parent和children,结点之上为parent，之下为children。位于同一结点的下的结点为sibling。
• order（度）：每个结点所拥有的最大children数，根据此定义，较为常见的二叉树得以命名。
• 分类：1.平衡树，所有叶子位于同一层或者至少彼此相差不超过一层。2.完全树，在平衡的基础上，底层所有叶子位于树的左边。3.满树，对于一个n元树，每层叶子都是满的，且均在同一层。

实现树的方法。

• 1.使用链表。
• 因为树的数据结构，每个结点指向其孩子，因此使用链表较为简单。
• 2.使用数组。
• • 根据二叉树的特殊性质，将左孩子存在数组（2 * n - 1 ） 索引值处，右孩子在（2 * n+1））处。但问题在于，当出现非满树的情况时，数组中的某些位置就必须空下以表示某parent只有一个孩子，当一个树大量存在这种情况时，将浪费大量的空间。
• • 模拟链接法。创建一个node型数组，使得每个元素存储下一个children的地址。问题，当删除一个结点时，如果不保留原结点位置，子结点移动时将会非常麻烦。如果只将其内部元素删除，保留内部结点的引用关系，又会占用空间。

树的遍历

• 前序遍历，中序遍历，后序遍历，层序遍历
• 前序遍历。从根节点开始，依次遍历至叶子处的左孩子，再依次由下至上返回由孩子。直到将整个树遍历完成。
  
• 中序遍历。从根结点开始。（注意，此时的从根节点开始并不是说第一个也就是根节点开始，而是从根节点到最后一个最左叶结点方向）从最左叶节点开始，至其parent结点，再至其右孩子。以此为规律，遍历整个树。
  
• 后序遍历。和中序遍历相同，从最左叶结点开始，然后至其兄弟结点。再至其parent结点。以此为规律，递归。
  
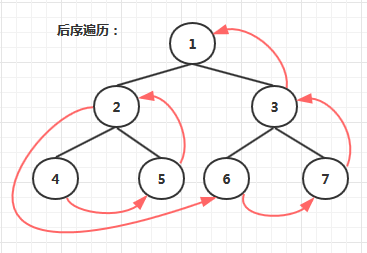
• 层序遍历。顾名思义，一层一层的遍历。从根节点开始。直到最后一层。
  

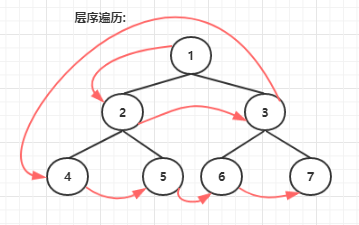
二叉树

• 二叉树。一个结点最多只有两个孩子。
• 二叉查找树。左孩子始终小于双亲，而双亲始终小于等于右孩子
• 二叉树的性质。
• • 若根结点的层次为1，则二叉树第i层最多有
    2^(i-1)(i>=1)个结点。
• • 在高度为h的二叉树中，最多有

2^h-1

个结点

教材学习中的问题和解决过程

• 问题1：对平衡二叉查找树的理解探究
• 问题1理解：
• 平衡树的定义：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。从这定义就可以看出具有递归的思想。
• 为什么需要使用二叉树？树作为一种非线性结构，并不以线性方式存储数据，这样一来，尤其是对于查找效率，将大大提高（从O(n)到O(logn)）。但当出现一些极端例子时，树的优势将不复存在，如图。

此时将一个顺序列表存入其中，树变为了右单子树或左单子树。问题出现了，此时的树直接变成了列表，查找效率也从O(logn)变为O(n)。为了解决这个问题，我们引入了平衡树的概念。如此，对于以无论何种顺序存入树的元素，不至于存的太深。在各个子树最多只能相差一的限制下，树的优势得以保留。

• 问题2：本章内容出现许多的迭代器与迭代器方法，对迭代器的探究。
• 问题2理解：
• 首先明确迭代的意义是什么。迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。
• 从概念上来看，迭代似乎与递归十分相似，都有着重复的过程。那么区别在哪呢？递归，简单的来说，就是自己调用自己，直到到达限制条件。递归并不是这样，递归通常有一个计数器，也就是通过循环不断进行计算，循环什么时候截止呢？在达到计数器时，结束循环。通过之前的代码可以知道，同一问题，递归实现的代码十分简洁可读。但循环体则较为复杂，对于一个复杂问题，短时间不易理解。但递归在带来代码简洁的同时，执行代码时将占用大量内存，稍有不慎会使得栈溢出，抛出异常。迭代则不会这样。
• 现在回到迭代器（Iterator）。内部有三个方法。hasnext，next，remove通过重写这三个方法，使得在不破坏内部结构的情况下，返回出内部的数据。

代码调试中的问题和解决过程

• 问题1：对于树中removeSubtree的方法
• 问题1解决方案：首先，明确要求，删除某一个右子树，直接将其设为null即可。问题在于，如何找到对应的右子树。是根据对应的那个元素判定还是对应的结点？其实都可以，代码如下：

if (next == null)
            return null;
        
        if (next.getElement().equals(targetElement))
            return next;
        
        BinaryTreeNode<T> temp = findNode(targetElement, next.getLeft());
        
        if (temp == null)
            temp = findNode(targetElement, next.getRight());
        
        return temp;

BinaryTreeNode<T> current = findNode(targetElement, root);
        
        if (current == null)
            throw new ElementNotFoundException("LinkedBinaryTree");
        
        return (current.getElement());

分别锁定了对应的位置和结点。因此任意调用这两个方法之一，即可找出相应的右子树。从而将其删除。删除时，将对应结点视为树的根，直接将根所在的LinkedBinary树等于null即可。

• 问题2：在测试contain方法时出现了异常的问题
• 问题2解决方案：测试之前，还出现了一段小插曲。如图，
  

显示了报错，同时无法执行代码。反复尝试无果后，发现之前使用栈实现了一个Postfixtest，而本章也有一个使用数实现的计算后缀表达式的程序，在将其重名的改名后，重启了几次idea后，如愿恢复了正常。我的理解是，首先idea必须保证所有程序不出错，否则其他程序编译将无法通过，同时，对于两个同名程序，无法判断执行哪个，因此选择不执行，知道将其改变。

• 根据抛出异常显示的位置，发现是removeSubRighttree出了问题，

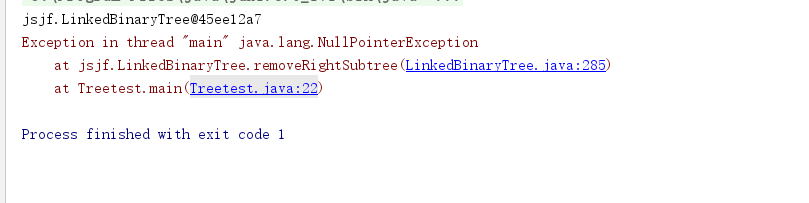
可是，抛出的是空指针异常，也就是并未找到所要删除的结点。所以问题不在这里。在于findnode方法，在方法体，我设置传入了一个的LinkedBinary的参数，但是，该树此时为空，自然将导致其为空指针。

• 解决了这个问题，再到contain方法，又出现了问题。依旧为空，仔细比对，发现了问题。在方法头，重新实例化了一个LinkedBinary对象，但是，其实树已经在之前方法确定，重新实例化反而相当于将其清空，造成空指针的情况。

代码托管

结对及互评

• 博客中值得学习的或问题：
  排版精美，对于问题研究得很细致，解答也很周全。
• 代码中值得学习的或问题：
  代码写的很规范，思路很清晰，继续加油！

点评过的同学博客和代码

• 本周结对学习情况
• 20172313
• 20172332

结对学习内容

• 第十章 树

其他（感悟、思考等，可选）

• 第一次学习非线性数据结构，对于某些知识还不是很了解，将继续对这些展开学习

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/0	1/1	3/3
第二周	409/409	1/2	5/8
第三周	1174/1583	1/3	10/18
第四周	1843/3426	2/5	10/28
第五周	539/3965	2/7	20/48
第六周	965/4936	1/8	20/68

参考资料

• 二叉查找树的删除算法的设计与实现递归与非递归
  
• 图解数据结构二叉树遍历