均衡直方图采所运用是是一个概率积分函数,对于某些像素个数很少,那么就需要压缩其存在的像素空间,甚至归于其他类像素点;对于某些像素个数很多,那么就需要延拓其存在的像素空间,这样看起来更加明显。概率积分函数为单调递增,形式如:
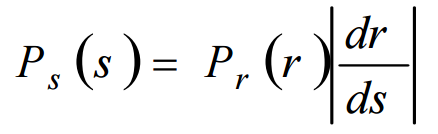
Pr(r)是r的概率密度函数,Ps(s)是s的概率密度函数。Pr(r)已知,在此处表示像素范围值,为255;dr表示像素值为小于等于s的个数,ds表示总的像素个数。最后化简成如下形式:

下面是运行代码:
需要说明:
【1】本程序实现的功能与OPenCV的 equalizeHist( src,dst )相同,但没有优化;
【2】运行中发现,map的执行速度远远不如vector容器。
【3】OpenCV中内置重新设置矩阵大小的函数 cv::resize
#include "opencv.h" void equalize(cv::Mat& src, cv::Mat& dst) { if (src.empty()) { cout << "Do not load image ..." << endl; return; } cv::resize(src, dst, cv::Size(src.cols, src.rows)); vector<int> s(256, 0); for (int i = 0; i < src.rows; i++) { const uchar* temp = src.ptr <uchar>(i); for (int j = 0; j < src.cols; j++) s[temp[j]]++; } int temp = 0; for (int i = 1; i < 256; i++) s[i] = s[i] + s[i - 1]; for (int i = 0; i < 256; i++) s[i] = (int)(1.0 * 256 * s[i] / s[255]); for (int i = 0; i < src.rows; i++) { uchar* temp = dst.ptr <uchar>(i); for (int j = 0; j < src.cols; j++) temp[j] = s[temp[j]]; } } //int main() //{ // string filename = "autum.jpg"; // cv::Mat src, dst; // src = cv::imread(filename); // cv::cvtColor(src, src, cv::COLOR_RGB2GRAY); // equalize(src, dst); // // cv::namedWindow("img", 0); // cv::imshow("img", src); // cv::namedWindow("equalize", 0); // cv::imshow("equaliize", dst); // cv::waitKey(); // return 0; //}