Jzzhu and Sequences CodeForces

题目链接

题意：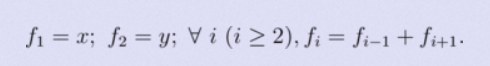

 给出这个式子的x和y，求fn

思路：很明显的矩阵快速幂，[fi,fi-1][{1,1}{-1,0}]=[fi+1,fi]

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=10;
const int mod=1e9+7;
struct Marix{//矩阵
    int mo[maxn][maxn],n;
    Marix(){}
    Marix(int _n){
        n=_n;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++) mo[i][j]=0;
        }
    }
};
Marix mul(Marix a,Marix b){//矩阵乘法
    Marix res=Marix(a.n);
    for(int i=0;i<a.n;i++){
        for(int j=0;j<a.n;j++){
            for(int k=0;k<a.n;k++){
                int tmp=(long long )a.mo[i][k]*b.mo[k][j]%mod;
                res.mo[i][j]=(res.mo[i][j]+tmp)%mod;
            }
        }
    }
    return res;
}
Marix powMod(Marix a,int n){//矩阵快速幂
    Marix nul;
    nul=Marix(a.n);
    for(int i=0;i<nul.n;i++){
        nul.mo[i][i]=1;
    }
    while(n){
        if(n&1) nul=mul(nul,a);
        a=mul(a,a);
        n>>=1;
    }
    return nul;
}
int main()
{
    int x,y,n;
    scanf("%d%d%d",&x,&y,&n);
    Marix t=Marix(2);
    t.mo[0][0]=1;
    t.mo[0][1]=1;
    t.mo[1][0]=-1;
    t.mo[1][1]=0;
    Marix t1=Marix(2);
    t1.mo[0][0]=y;
    t1.mo[0][1]=x;
    Marix ans1=powMod(t,n-1);
    Marix ans=mul(t1,ans1);
    printf("%d
",(ans.mo[0][1]+mod)%mod);
 }