一般素数的求法有两种,一种是埃氏筛法,还有一种是线性筛(即欧拉筛法)。
埃氏筛法(时间复杂度O(nlognlogn))
给出要筛数值的范围 n,找出 n以内的素数p1,p2,p3,......,pk。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个素数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个素数5筛,把5留下,把5的倍数剔除掉;不断重复下去......。
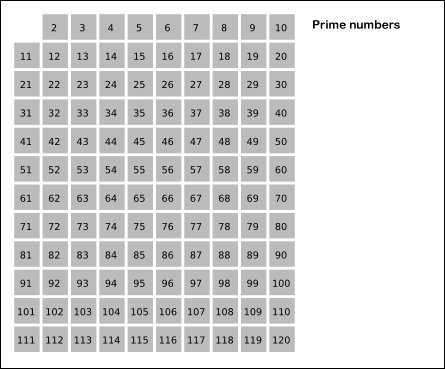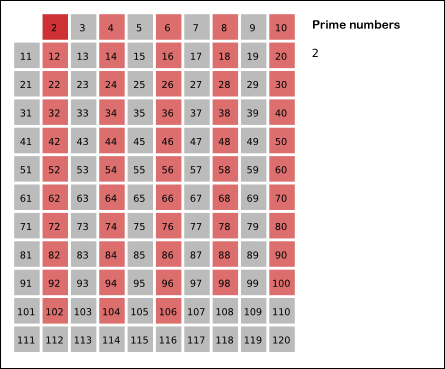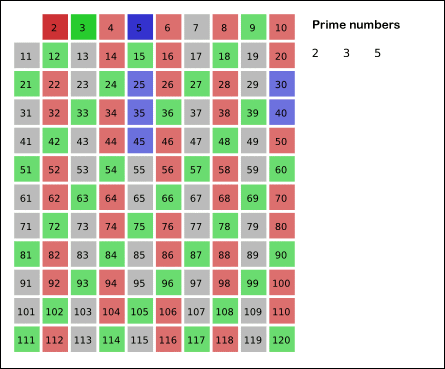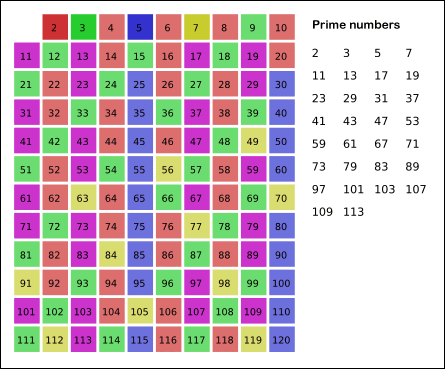
int m = sqrt (n + 0.5); memset(vis,0,sizeof(vis)); for(int i=2;i<=m;i++) if( !vis[i] ) for(int j=i*i;j<=n;j+=i) vis[j]=1;
用一个数组来储存素数表
int m = sqrt (n + 0.5); // n + 0.5解决精度问题 memset(vis,0,sizeof(vis)); memset(prime,0,sizeof(prime)); int cnt=1,i; for(i=2;i<=m;i++) if( !vis[i] ){ prime[cnt++]=i; for(int j=i*i;j<=n;j+=i) vis[j]=1; } for(;i<=n;++i){ if(!vis[i]) prime[cnt++]=i;
欧拉筛法(O(n))
埃氏筛法的问题在于他把每个合筛了不只一次,所以我们需要通过优化来使每个合数只需要一遍就能被筛出来,即为欧拉筛法
for( int i = 2 ; i <= n ; ++i ){ if( IsPrime[ i ] ) Pri[ PriN++ ]=i; //将这句话放在下面的循环前以保证PriN和Pri值的完整性 for(int j=0;j<PriN;++j){ if( i*Pri[ j ] > MaxN ) break; //当过大了就跳出 IsPrime[ i * Pri[ j ] ] = 0; //筛去素数 if( i % Pri[ j ] == 0 ) break; //这里是关键,如果i是一个合数(这当然是允许的)而且i mod prime[j] = 0 //那么跳出,因为i*prime[ (- over -)j ]一定已经被筛去了,被一个素因子比i小的数 } }