03-树1 树的同构 (25分)
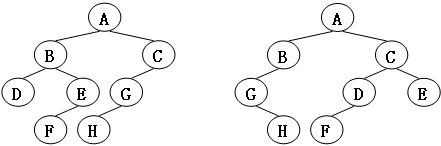
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
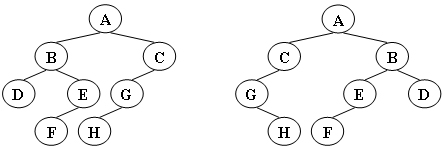
图1
图2
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8 A 1 2 B 3 4 C 5 - D - - E 6 - G 7 - F - - H - - 8 G - 4 B 7 6 F - - A 5 1 H - - C 0 - D - - E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8 B 5 7 F - - A 0 3 C 6 - H - - D - - G 4 - E 1 - 8 D 6 - B 5 - E - - H - - C 0 2 G - 3 F - - A 1 4
输出样例2:
No
提交源代码:
#include <stdio.h> #include <stdlib.h> #define MAXSIZE 10 #define Null -1 typedef char ElemType; typedef int Tree; struct TreeNode { ElemType element; Tree left; Tree right; }T1[MAXSIZE], T2[MAXSIZE]; Tree BuildTree(struct TreeNode T[]) { int N; scanf("%d ", &N); if( N == 0) return Null; int *check = (int*)malloc(sizeof(int) * N); for (int i = 0; i < N; ++i) { check[i] = 0; } char cl, cr; for (int i = 0; i < N; ++i) { scanf("%c %c %c ", &(T[i].element), &cl, &cr); if (cl != '-') { T[i].left = cl - '0'; check[T[i].left] = 1; } else { T[i].left = Null; } if (cr != '-') { T[i].right = cr - '0'; check[T[i].right] = 1; } else { T[i].right = Null; } } Tree root; for (int i = 0; i < N; ++i) { if (check[i] == 0) { root = i; break; } } return root; } int Isomorphic(Tree R1, Tree R2) { if (R1 == Null && R2 == Null) { return 1; } if ((R1 == Null && R2 != Null) || ((R1 != Null) && (R2 == Null))) { return 0; } if (T1[R1].element != T2[R2].element) { return 0; } if (T1[R1].left == Null && T2[R2].left == Null) { return Isomorphic(T1[R1].right, T2[R2].right); } if (((T1[R1].left != Null) && (T2[R2].left != Null)) && (T1[T1[R1].left].element == T2[T2[R2].left].element)) { return (Isomorphic(T1[R1].left, T2[R2].left) && Isomorphic(T1[R1].right, T2[R2].right)); } else { return (Isomorphic(T1[R1].left, T2[R2].right) && Isomorphic(T1[R1].right, T2[R2].left)); } } int main() { Tree root1 = BuildTree(T1); Tree root2 = BuildTree(T2); if (Isomorphic(root1, root2)) { printf("Yes"); } else { printf("No"); } return 0; }
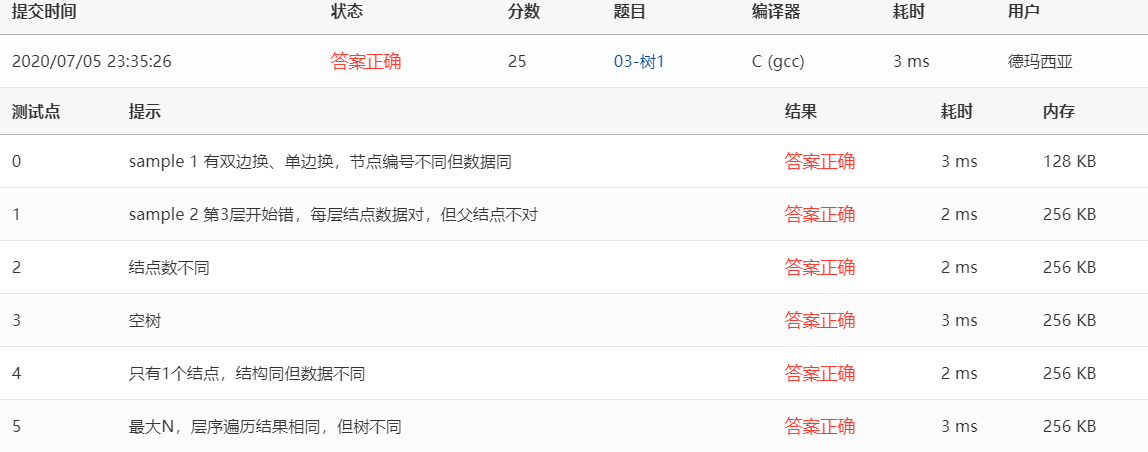
提交代码结果: