20135202闫佳歆——家庭作业汇总

第二章家庭作业

选题：2.69

分值：三分

作业过程：

以下是rotate_right函数的代码：

unsigned rotate_right(unsigned x, int n)
{
	int endbit;
	int i;
	if(n==0)
		return x;
	else
	{
		for(i=0;i<n;i++)
		{
			endbit = x & 0x1;
			endbit = endbit << (8*sizeof(unsigned)-1);
			x = x >> 1;
			x = x | endbit;
		}
	}
	return x;
}

这里用到的原理是，区分n的情况，如果是0则直接返回原值，如果不是0，就按照移位的次数控制循环，每次循环只移位1位。

具体循环的实现，是借助了一个变量为endbit，最后一位，用来保留右移一位后损失掉的那位，再通过移位使这位变成最高位，最后与x移位后的数据进行或运算，这样就完成了循环右移一次的功能；共需循环右移几次，就重复几次这个循环。

完成的代码如下：

#include <stdio.h>

unsigned rotate_right(unsigned x, int n);

int main()
{
	int n = 0;
	unsigned x;
	int w = sizeof(unsigned)*8;
	int flag = 0;
	unsigned result;

	while(!flag)
	{
		printf("please input how many bits you want to rotate_right shift:
");
		scanf("%d",&n);
		if (n < 0 || n >= w)
		{
			printf("Wrong! Please input again!
");
		}
		else
			flag = 1;
	}

printf("please input your data:
0x");
	scanf("%x",&x);

	result = rotate_right(x,n);
	printf("the result is:0x%x
",result);

	return 0;
}

unsigned rotate_right(unsigned x, int n)
{
	int endbit;
	int i;
	if(n==0)
		return x;
	else
	{
		for(i=0;i<n;i++)
		{
			endbit = x & 0x1;
			endbit = endbit << (8*sizeof(unsigned)-1);
			x = x >> 1;
			x = x | endbit;
		}
	}
	return x;
}

实验运行结果如下：

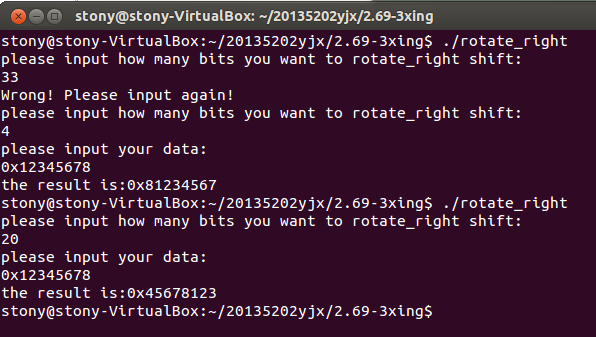
实验中遇到的问题：

这个函数原型的构造并不难，找到思路后困扰我一时的只是是用或还是与，这个很容易就能够解决，更大的问题在我的主函数中输入无论如何都得不到正确的结果，后来发现是因为我的输入是0x12345678，我以为这个可以直接转换为16进制但是不可以，输出也是十进制，所以这导致了我的结果错误百出，后来我通过百度发现了%x的方法，输入输出格式改为这个之后就可以方便的输入输出16进制，并且在输入之前加了提示语0x，就可以得出正确的结果了。

这道题本身难度不算大，我主要还是栽在了自己的粗心上，没有注意输入输出格式，只想当然的去做，吸取了这次教训，以后的作业就不会有那么多冤枉路了。

代码的优化

从每次右移一位，按循环次数控制右移位数，能不能扩展成一步到位移动n位呢？我把代码变成了以下样子：

unsigned rotate_right(unsigned x, int n)
{
	int endbit;
	int i;
	if(n==0)
		return x;
	else
    {
	    endbit = x << (8*sizeof(unsigned)-n);
	    x = x >> n;
	    x = x | endbit;
    }
	return x;
}

这样就可以直接移动n位了。

这里还有一个小插曲，关于开始的左移位数是要-n还是-什么，是右移了n位，上面的左移就要减n。

然后我又想，n=0的情况能不能并进去？代码就变成了这样子：

unsigned rotate_right(unsigned x, int n)
{
	int endbit;

    endbit = x << (8*sizeof(unsigned)-n);
    x = x >> n;
    x = x | endbit;

	return x;
}

验证是可以的。

endbit作为一个中间值，是不是有点多余？去掉之后变成：

unsigned rotate_right(unsigned x, int n)
{
    x = (x >> n) | x << (8*sizeof(unsigned)-n);

	return x;
}

也是可以的，更简洁了。

那么可以干脆直接用return返回：

unsigned rotate_right(unsigned x, int n)
{
    return (x >> n) | x << (8*sizeof(unsigned)-n);
}

这个一步步简化代码的过程让我做完了之后十分满意，最开始的想法很简单，但是代码实现却很复杂，通过一步步的简化最终使代码变的简洁好看，成就感很大。但是对于我现在的水平，如果直接给我这样的一个代码，阅读起来还是有些费劲的，需要多加练习。

第三章家庭作业

选题：3.63

分值：两分

作业过程：

原来的函数：

int sum_col(int n,int A[E1(n)][E2(n)],int j)
{
	int i;
	int result = 0;
	for(i=0;i<E1(n);i++)
		result += A[i][j];
	return result;
}

转化为goto代码的版本：

int sum_col(int n,int A[E1(n)][E2(n)],int j)
{
	int i=0;
	int result = 0;
	if(!(i<E1(n)))
		goto done;
loop:
	result += A[i][j];
	i++;
	if(i<E1(n))
		goto loop;
done:
	return result;
}

在书中给的汇编代码中，逐句分析如下：

	movl	8(%ebp),%edx	   ;把ebp+8中的值赋给edx，也就是n
	leal	(%edx,%edx),%eax   ;eax中的值等于两倍的edx中的值，即2n
	leal	-1(%eax),%ecx	   ;ecx中的值等于eax中的值-1，即2n-1
	leal	(%eax,%edx),%esi   ;esi中的值等于eax的值加edx的值，即3n，esi存储的是E1(n)的值
	movl	$0,%eax		   ;eax置零，eax存储的是result的值
	testl	%esi,%esi	   ;检查esi中的值是正、负还是0
	jle		.L3	   ;因为初始化i是0，如果esi中的E1(n)≤0的话，就满足!(i<E1(n))跳转到done
	leal	0(,%ecx,4),%ebx	   ;ebx中的值等于0+4*ecx=4（2n-1）
	movl	16(%ebp),%eax	   ;eax中的值等于ebp+16，即j的地址
	movl	12(%ebp),%edx	   ;edx中的值等于ebp+12，即A[i]的地址
	leal	(%edx,%eax,4),%ecx ;ecx中的值等于[edx+4*eax]中的值，即A[i][j]
	movl	$0,%edx		   ;edx中的值置零
	movl	$0,%eax		   ;eax中的值置零
.L4				   ;相当于loop
	addl	(%ecx),%eax	   ;eax中的值+=ecx中的地址，即A[i][j]的地址
	addl	$1,%edx		   ;edx中的值加一，可以看出edx存放的是i
	addl	%ebx,%ecx	   ;ecx中的值加上ebx中的值放到ecx中，即ecx内值为A[i+1][j]
	cmpl	%esi,%edx	   ;比较esi与edx中的值，即比较E1(n)和i的值
	jl		.L4	   ;如果i<E1(n)，跳转回.L4，相当于回到loop中的循环
.L3				   ;相当于done，结束

所以，由上面的逐句分析可得，esi中存储的是E1(n)的值，E1(n)=3n；
E2(n)储存在ebx中，ebx=4*E2(n)，所以E2(n)=2n-1.

总结

这道题锻炼了我对汇编语言的分析过程，知道每一句对应的动作，不同指令的用法，寄存器中的数值的变化等等；同时还练习了for循环是如何在汇编中被实现的，这道题如果直接对着原函数分析不好分析，但是转变为goto形式的代码后就比较直接、一目了然

第四章家庭作业

选题：4.47、4.48两题

分值：两题各一分

作业过程：

4.47题：

leave指令等价于如下代码序列：

rrmovl	%ebp,%esp
popl	%ebp

也就是说它要执行的动作是，将帧指针ebp的内容赋给栈指针esp，然后弹出ebp，栈指针+4，结果是消灭这个栈。

参照pop指令的格式，可以得出如下的过程：

取指阶段   icode:ifun<--M1[PC] = D:0
		
        valP <= PC + 1	;下一条指令地址

译码阶段   valB <= R[%ebp]   ;得到ebp的值，这个值就是新的栈指针esp的值

执行阶段   valE <= valB + 4   ;栈指针的值+4

访存阶段   valM <= M4[valB]   ;读ebp中的值

写回阶段   R[%esp] <= valE   ;把更新后的指针赋值给esp
           R[%ebp] <= valM   ;弹出的ebp的值

4.48题

iaddl的指令是集合了irmovl指令和addl指令，先用irmovl指令将一个常数加到寄存器，再用addl把这个值加入目的寄存器。

由题中的图，参考irmovl和addl指令的过程，可以得到如下过程：

取指阶段   icode:ifun = M1[PC] = C:0
        
	   rA:rB <= M1[PC+1]   ;取出操作数指示符
           valC <= M4[PC+2]   ;取出一个四字节常数字，即想要加进去的那个常数
           valP <= PC + 6   ;下一条指令地址

译码阶段   valB <= R[rB]   ;读入想要存到的那个寄存器

执行阶段   valE <= valB + valC   ;得到目的寄存器中的值和常数值的和
           SetCC

访存阶段  

写回阶段   R[rB] <= valE   ;把结果写回到目的寄存器中。

感想

这次的作业难度比较低，主要是复习了对顺序实现的几个步骤里都做了些什么，每一步都代表着什么意义，练习熟练后可以做到举一反三。

第六章家庭作业

分值分配

6.28:20135202(1.5) 20135220(0.5)

6.37:20135202(1) 20135220(3)

6.38:20135202(3) 20135220(1)

6.28 分值1分

（1）所有会在组6中命中的十六进制存储器地址：

由习题6.13的表可知，如要命中组六，需要标记位为91，组为6，也就是说八个CT位的值分别为1001 0001，三个CI的值为110，剩下两位是任意的，取值范围为00,01,10,11，所以所有的情况只有四种：

1 0010 0011 1000 = 0x1238

1 0010 0011 1001 = 0x1239

1 0010 0011 1010 = 0x123A

1 0010 0011 1011 = 0x123B

（2）命中组1的：同上题相同，八个CT值分别为0100 0101，三个CI值分别为001，有四种情况：

0 1000 1010 0100 = 0x08A4

0 1000 1010 0101 = 0x08A5

0 1000 1010 0110 = 0x08A6

0 1000 1010 0111 = 0x08A7

6.37 分值2分

题目

C程序：

int x[2][256];
int i;
int sum=0;

for (i=0;i<256;i++){
	sum += x[0][i] * x[1][i];
}

• sizeof(int) == 4

• 数组X从存储器地址0x0开始，按照行优先顺序存储。

• 每种情况中，高速缓存最开始时都是空的。

• 唯一的存储器访问是对数组x的条目进行访问，其他所有变量都存储在寄存器中。

A、假设高速缓存是1024字节，直接映射，高速缓存块大小为32字节，不命中率是多少？

直接映射是每组只有一个高速缓存行，块大小为32字节，表示可以存储8个int数值。
数组是按照行优先存储的，计算数组一行的大小为256*4=1024，所以高速缓存只够存数组的一行。
所以x[0]和x[1]的每一个元素（x[0][i]和x[1][i]）对应的高速缓存是同一个块。
因此，每次请求都在加载，驱逐，替换。不命中率为100%。

B、高速缓存改为2048字节，不命中率是多少？

缓存足够大，可以存储整个数组
因此只有冷不命中，而块大小为32字节，表示可以存储8个int数值
所以每次都会加载x[0][i]~x[0][i+7]共8个数值到缓存组中，这里就只有x[0][i]是不命中的
所以不命中率为1/8 = 12.5%

C、高速缓存是1024字节，两路组相联，使用LRU替换策略，高速缓存块大小为32字节，不命中率是多少？

两路组相联表示每组有两个高速缓存行，而每行可以存储8个数值
高速缓存只有1024字节，不够存储数组
发生不命中的时候，一个是冷不命中，另一个是缓存中没有，需要加载进去
这时使用的是LRU替换策略，替换最近最少用的，替换的那一行的8个数值已经都用过了，再也不会用到了
所以最后还是相当于只有冷不命中，相当于每8个数据中只有一个是不命中的
所以不命中率为1/8 = 12.5%

D、C中，更大的高速缓存大小会帮助降低不命中率吗？

不会，因为块大小不变时，冷不命中的概率不可能被减小。

E、C中，更大的块大小会帮助降低不命中率吗？

会降低，因为一个块的大小增加，冷不命中的频率就降低。

6.38 分值2分

解：

由题意可知，C=4KB=4096 Bytes，而C = S x E x B，在直接映射高速缓存中E = 1，块大小B=16 Bytes，可得S = 256，一共有256个高速缓存组。

（1）N = 64时：

数组大小为2x64x4=512字节，缓存容量足够大，不用考虑容量不命中。
因为每块是16字节，数组中每个单元为4字节，所以四个一组，一共需要16组，每一组中的行都是满的

sumA步长为1，遵循了行优先顺序，这个里面只有冷不命中，就是四个中有一个不命中，不命中率为0.25

sumB是列优先，步长为N，每一次都会与上一次的映射到同一个块，导致每次都会冲突，所以不命中率为1

sumC中除了四个中有一个冷不命中外，还因为列扫描到i+1时的冲突不命中（每次都会映射到同一组同一块），所以不命中率为0.5

（2）N = 60时：

数组大小为2x60x4=480字节，缓存容量足够大，不用考虑容量不命中。
因为每块是16字节，数组中每个单元为4字节，所以四个一组，一共需要16组，但行中不是满的

sumA同上，只有冷不命中，不命中率为0.25

sumB消除了冲突不命中，不会每次都映射到同一组同一块，所以只有冷不命中，不命中率为0.25

sumC理由同上，只有冷不命中，不命中率为0.25

第十章作业

题目：10.8

编写图10-10中的statcheck程序的一个版本，叫fstatcheck，它从命令行上取得一个描述符数字而不是文件名。

分值：2分

解题过程：

图10-10代码如下：

#include "csapp.h"

int main (int argc, char **argv) 
{
    struct stat stat;
    char *type, *readok;
    
    if (argc != 2) {
    	fprintf(stderr, "usage: %s <filename>
", argv[0]);
    	exit(0);
    }
    
    Stat(argv[1], &stat);//这句是从命令行中读取一个文件名
    if (S_ISREG(stat.st_mode)) 
    	type = "regular";
    else if (S_ISDIR(stat.st_mode))
    	type = "directory";
    else 
    	type = "other";
    if ((stat.st_mode & S_IRUSR)) /* Check read access */
    	readok = "yes";
    else
    	readok = "no";
    
    printf("type: %s, read: %s
", type, readok);
    exit(0);
}

题目要求是从命令行读取的内容从文件名改为描述符数字。那就先找到这个取得文件名的代码，是

Stat(argv[1], &stat);

这一句中argv就是用来去输入的信息的，取出放到stat中。所以只需要更改这一句即可，需要的是一个将字符串转换为整型数的函数，经过查询百度后找到了atoi函数，所以这句话修改为：

fstat(atoi(argv[1]), &stat);

即可。