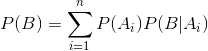一、概率
1、定义:
对于古典试验中的事件A,它的概率定义为:P(A)=m/n,其中n表示该试验中所有可能出现的基本结果的总数目。m表示事件A包含的试验基本结果数。
由于频率nA/n总是介于0和1之间,从概率的统计定义可知,对任意事件A,皆有0≤P(A)≤1,P(Ω)=1,P(Φ)=0。其中Ω、Φ分别表示必然事件(在一定条件下必然发生的事件)和不可能事件(在一定条件下必然不发生的事件)。
2、满足条件:
(1)非负性:对于每一个事件A,有P(A)≥0;
(2)规范性:对于必然事件Ω,有P(Ω)=1;
(3)可列可加性:设A1,A2……是两两互不相容的事件,即对于i≠j,Ai∩Aj=φ,(i,j=1,2……),则有P(A1∪A2∪……)=P(A1)+P(A2)+……
3、名词:
随机事件:在一定的条件下可能发生也可能不发生的事件,叫做随机事件。
可能事件:通常一次实验中的某一事件由基本事件组成。如果一次实验中可能出现的结果有n个,即此实验由n个基本事件组成,而且所有结果出现的可能性都相等,那么这种事件就叫做等可能事件。
互斥事件:不可能同时发生的两个事件叫做互斥事件。
对立事件:即必有一个发生的互斥事件叫做对立事件。
4、性质:
性质1.P(Φ)=0.
性质2.(有限可加性)当n个事件A1,…,An两两互不相容时: P(A1∪...∪An)=P(A1)+...+P(An)
性质3.对于任意一个事件A:P(A)=1-P(非A)
性质4.当事件A,B满足A包含于B时:P(B-A)=P(B)-P(A),P(A)≤P(B)
性质5.对于任意一个事件A,P(A)≤1
性质6.对任意两个事件A和B,P(B-A)=P(B)-P(AB)
性质7.(加法公式)对任意两个事件A和B,P(A∪B)=P(A)+P(B)-P(A∩B)
5、其它:
p(AB)是指AB两事件同时出现的概率。
A,B相互独立:P(AB)=P(A)P(B)
A,B不是相互独立:P(AB)=P(B|A)*P(A)
P(A│B)是指在已经发生B的条件下,再发生A事件出现的概率。P(A│B)= P(AB)/ P(B)
先验概率:由以往的数据分析得到的概率, 叫做先验概率。
后验概率:而在得到信息之后,再重新加以修正的概率叫做后验概率。
6、贝叶斯分类算法
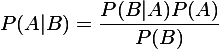
7、全概率公式:公式表示若干事件A1,A2,…,An构成一个完备事件组且都有正概率,则对任意一个事件B都有公式成立。