题目大意
LSZ很皮!LSZ的皮肤衣更皮!
LSZ有很多件神奇的皮肤衣,而且LSZ总是喜欢一次穿上多件皮肤衣(一件套一件,而且一直穿好多天),这些皮肤衣有透明或不透明两种状态,当不透明的皮肤衣吸收了一天的阳光直射后,就会变成透明的皮肤衣,透明的皮肤衣能使阳光照射到里层皮肤衣,而透明的皮肤衣再吸收阳光,会在第二天会变成不透明的皮肤衣,不透明的皮肤衣会阻止阳光照射到里层皮肤衣。
LSZ从某天起(该天算作第1天)穿上N(N <= (4*10^{9}))件皮肤衣(刚开始所有皮肤衣都是不透明的),问你最少要经过多少天,LSZ身上的皮肤衣都经历过透明变化?
例如今天(公元2018年6月17日)LSZ穿了3件皮肤衣服,会在公元2018年6月21日3件皮肤衣都会经历过透明变化。
输入格式
一行,只有一个整数N。
输出格式
最少的天数(对N取余数)
样例
样例输入
3
样例输出
2
样例解释
- 使用0代表皮肤衣透明状态。
- 使用1代表皮肤衣不透明的状态。
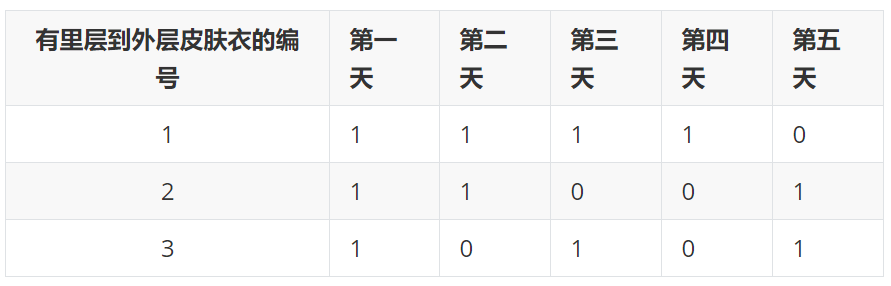
5对3取余数为2。
算法分析:
这个题算是一个比较裸的数论的题了吧,很显然的式子,先来定义一个数组f[i]表示有i个衣服要变透明所需要的天数
- 如果我们要求f[n] :我们只需要把第n个变成0就可以了 前提是将前n-1个由1变成0 假设我们已经知道了前n-1个由1变成0需要的天数为x 则f[n]就是下x+1
- 如果求f[n+1]呢:那么我们再去推第n+1个变成0的天数 前提是前n个变成0的时间 前n个都是0需要 前n-1个变成0 然后第n个变成0 然后前n-1个再变成0 然后再加1(使第n+1个变成0)所以f[n+1] = x+1+x = 2(x+1)-1 = 2f[n]-1
- 将f[n+1]和f[n]建立关系了 但是对于(4*10^{10})这样大的数据显然无法通过递推求解,所以我们需要一个通式,先来f[1] = 2 ,f[2] = 3,通过一点点数学方法(等比数列加代换
或者直接眼暴)很容易就知道f[n] = (2^{n-1} - 1) - 然后就可以求解了 那我们的主要问题就变成了怎么求(2^{n-1}-1) (
显然快速幂呗) - 然后就是个快速幂板子了
代码展示
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll power(ll a,ll b,ll p){
ll ans = 1%p;
for(;b;b>>=1){
if(b&1)ans = ans*a%p;
a = a * a % p;
}
return ans;
}
int main(){
ll n;scanf("%lld",&n);
ll ans = power(2,n-1,n);
ans = (ans + 1)%n;
printf("%lld",ans);
return 0;
}
谢谢观看
点个关注
_<