摘要
写作动机:毕业设计是从头写一个3D渲染器,编程语言为Rust。鉴于有幸听过GAMES101相关课程,遂想为毕设加入4xMSAA抗锯齿算法。但踩了几个大坑,差点自闭,解决后趁思路还算清晰,分享一下遇到的难点和对应方案。
这三篇博文给了我较大启发:
另外,本文并不会教你MSAA的原理,讨论仅从我在实现时应用的方案来切入。
问题的产生
接触过GAMES101 CG课作业二的伙伴应该熟悉,课程定义的MSAA流程以及我们在网上看到的实现如下:
// 't'为当前三角形面片
seg_pos = {{0.25, 0.25}, {0.75, 0.25},{0.25, 0.75}, {0.75, 0.75}};
for(int x=x_l;x<=x_r;x++)
for(int y=y_b;y<=y_t;y++)
int count = 0
float min_depth = FLT_MAX;
for(auto & e : seg_pos)
if(insideTriangle((float)x + e[0], (float)y + e[1], t.v))
count++
...用重心坐标插值出当前采样点深度
min_depth = std::min(min_depth, 当前采样点深度)
if(count != 0 && depth_buf[get_index(x, y)] > min_depth)
像素颜色 = t.getColor() * (count / 4)
设置颜色(像素颜色)
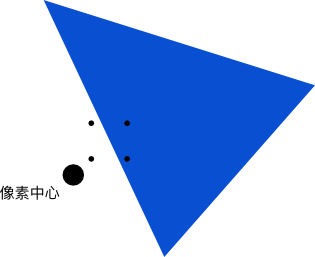
这是一种简化版MSAA:四个子采样点设置在像素中心的右上角,判断每个采样点是否在当前考虑的三角形面片内,若是则命中次数加1,并维护一个变量min_depth,记录四个采样点中最小的深度值。如果命中次数为0,或者未通过深度测试,则直接discard当前像素;否则当前像素设置颜色为 三角形颜色 * 命中率,说白了就是简单的算术平均。
于是乎,我为毕设实现MSAA时便屁颠屁颠地直接将上述流程照搬,结果出了大问题 -- 每个三角形面片之间出现了黑色裂缝:

一开始我以为又是什么舍入带来的精度损失,查阅资料后,好像在实现GAMES作业2的时候也有类似问题。
于是我重新回去运行作业2,确实在三角形交界处会出现黑线:

直接原因便是,这种算法存在一个缺陷,具体请看图:

(注意,作业2比较特殊,整个场景就定义了两个三角形面片,也就是蓝色和黄绿色三角形)
图中,我们正在蓝色三角形内进行光栅化。考虑一种最坏的情况,即边缘像素仅有左下角的采样点命中了蓝色三角形内部。
按照上面伪代码的思路,根本不考虑另外三个处于黄绿色三角形内的采样点的贡献,当前像素颜色简单粗暴设置为 t.getColor() * (1/4) ,这里的 (t) 即为蓝色三角形,它的颜色为 (RGB(194,217,233)),则当前像素会被设置为 (RGB(48,54,58)),呈现出一种类似于黑色的颜色,所以也不难想象当采样点命中为2、3个的时候,颜色也只是会稍微浅一点罢了,这与右边的黄绿色产生了一种较强的割裂感,从而产生裂缝的错觉。
尝试解决
意识到问题后,我便查阅资料,并确定要实现一种开销较大的MSAA:
每个像素有4bit的coverage mask,以及4个深度值(每个sample各一个),另外还有其他attribute(最简单的就是color),并且是可以拿一份color copy给所有sample(准确地说是只copy给那些mask非0的sample),而这份color可以来自像素中心或者某个sample。
策略
我选用的策略是,对于一个像素,算出其每个被命中sample(采样点)的颜色、深度,最后再对相关值进行关于命中次数的算术平均:
(这个例子和上述作业2不太一样,这里假设背景的蓝色和黄绿色仅恰巧为某些材质的接缝处,并不是简单的两个三角形交界;图中的三角形是很多三角面片的其中一个)
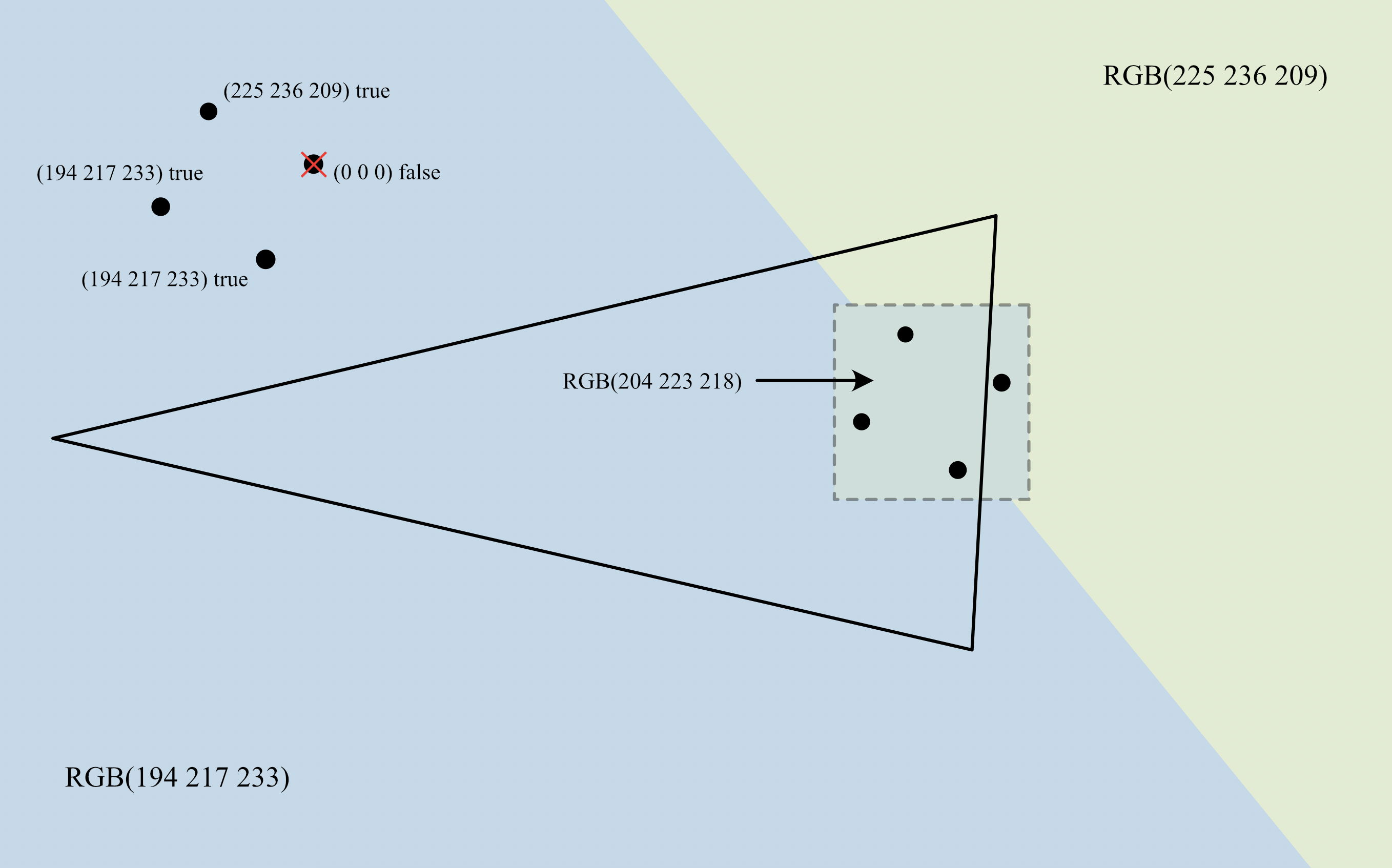
如图,按照我选择的策略,该像素最右的sample在该三角形之外,被discard(丢弃)。那么该像素的颜色即为剩下三个sample颜色的算术平均,最终颜色在边界处产生一种较为平滑的过渡。这其实接近于SSAA了,因为会对多个采样点运行fragment shader。
实现
你可能会注意到我在讲述策略时用了一种不太一样的sample模式,也即采样点并非在像素右上角,而是环绕像素中心并略微旋转:

因为在应对三角形边界情形时,顺时针旋转26.6度的算子被证明是一种比较有效的sample模式。下面来看如何通过代码一步步实现:
为了得到目标模式,我们先确立一个正正方方的采样模式,其各sample都是一个Vector2类型,为这些sample均乘以一个旋转矩阵即可:

pub static MSAA_LEVEL: usize = 4;
pub static MSAA_OFFSET: f32 = 0.25;
pub static MSAA_SAMPLE_POS: Matrix2<Vector2<f32>> = Matrix2::new(
Vector2::new(-MSAA_OFFSET,-MSAA_OFFSET),Vector2::new(MSAA_OFFSET,MSAA_OFFSET),
Vector2::new(-MSAA_OFFSET,MSAA_OFFSET),Vector2::new(MSAA_OFFSET,-MSAA_OFFSET),
);
- MSAA_LEVEL表征一个像素的sample个数
- MSAA_OFFSET表征每个sample与像素中心x、y的偏移绝对值
- MSAA_SAMPLE_POS表征还未旋转的sample模式
计算旋转后的模式:
pub fn calc_conv() -> Matrix2<Vector2<f32>> {
let mut conv_tmp: Matrix2<Vector2<f32>> = Default::default();
let rotate: Matrix2<f32> = rotate_matrix2d(-26.6);
for i in 0..4 {
conv_tmp[i] = rotate*MSAA_SAMPLE_POS[i];
}
conv_tmp
}
为了方便输出单个像素四个sample的状态,我定义了一个结构叫做 MsaaTensor
pub struct MsaaTensor {
mask: Vector4<bool>,
dept: Vector4<f32>,
colo: Vector4<Vector3<f32>>,
}
- mask记录各sample是否被激活(命中 / hit)
- dept记录各sample的深度
- colo记录各sample的颜色
进入渲染例程,通过三个变量奠基:
for 像素(x,y) in 当前三角形包围盒 {
let 像素坐标 = x + y * self.height;
let 张量 = msaa_tensors[像素坐标];
let hit = 0.0;
......
}
为每个像素计算其MsaaTensor四个角的信息:
for 像素(x,y) in 当前三角形包围盒 {
......
for idx in 0..MSAA_LEVEL {
let 采样点重心坐标 = barycentric(三角形三顶点,像素.x+采样模式[idx].x,像素.y+采样模式[idx].y);
if 在三角形内(采样点重心坐标) {
hit += 1.0;
let 深度 = 深度插值(采样点重心坐标,三角形三顶点);
tensor.设置标志(idx,true);
tensor.设置深度(idx,深度);
tensor.设置颜色(idx,着色器.颜色(采样点重心坐标));
}else {
tensor.设置标志(idx,false);
}
}
......
}
如果没有子sample被hit,那么直接discard此像素:
for 像素(x,y) in 当前三角形包围盒 {
......
if hit == 0.0 {
continue;
}
......
}
只要有一个sample被hit,计算blend信息并着色:
for 像素(x,y) in 当前三角形包围盒 {
.......
else {
let 漫反射_blend = Default::default();
let 深度_blend = 0.0;
for idx in 0..MSAA_LEVEL {
if msaa_tensors[ipixel].标志位(idx) == true {
漫反射_blend += msaa_tensors[ipixel].颜色(idx);
深度_blend += msaa_tensors[ipixel].深度(idx);
}
}
// 当前pixel的深度由被hit的子sample混合得到
深度_blend /= hit;
if 深度缓存(像素.x,像素.y)>深度_blend {
continue;
}
深度缓存(像素x, 像素.y, depth_blend);
帧缓存(像素.x, 像素.y, 漫反射_blend/hit);
}
......
}
运行程序看看效果:
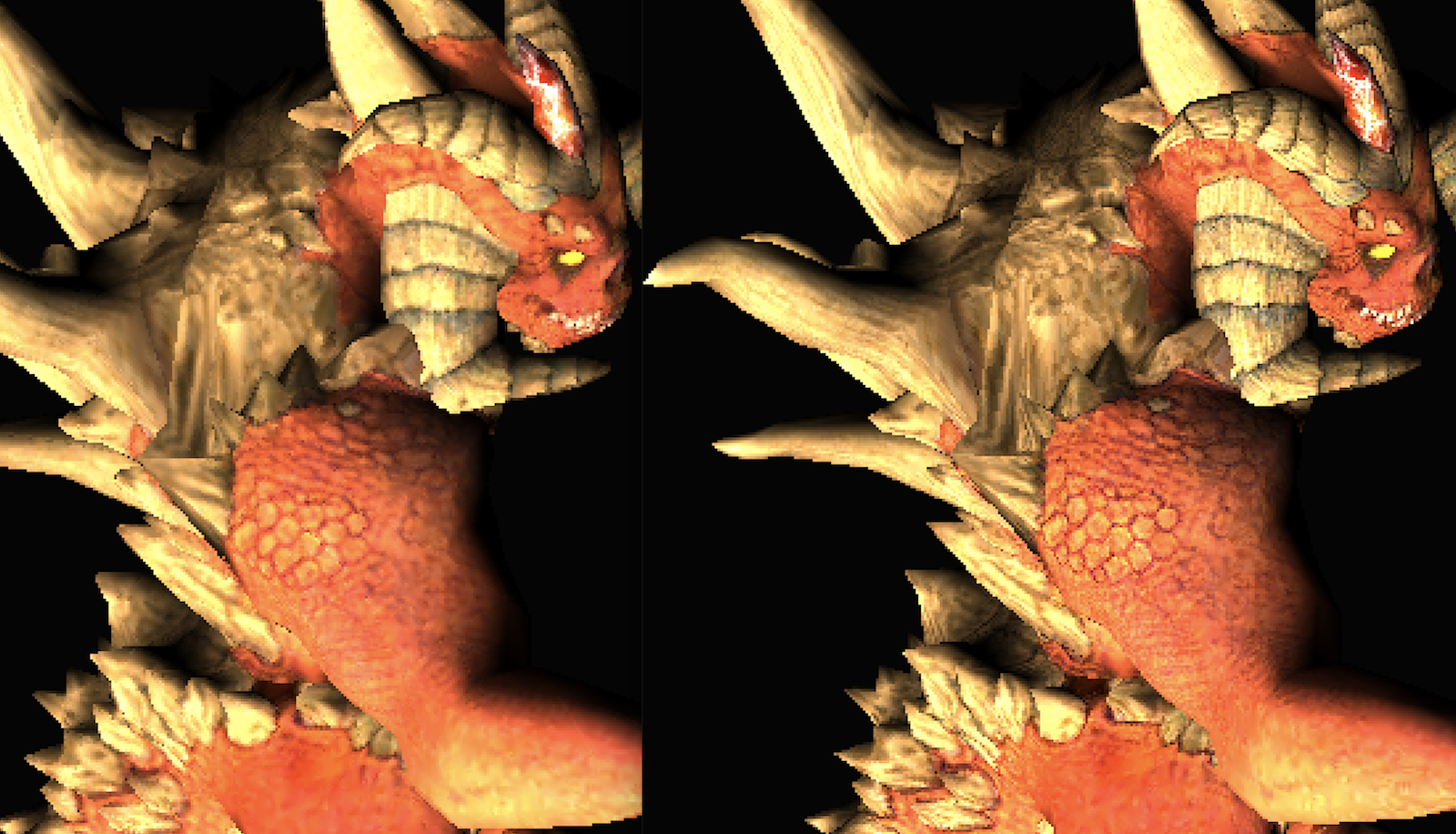
对比发现,好像除了一些地方变糊了,模型内部颜色交界处改善不太明显。那么试着把MSAA_OFFSET的步长改大一点:
pub static MSAA_OFFSET: f32 = 0.5;
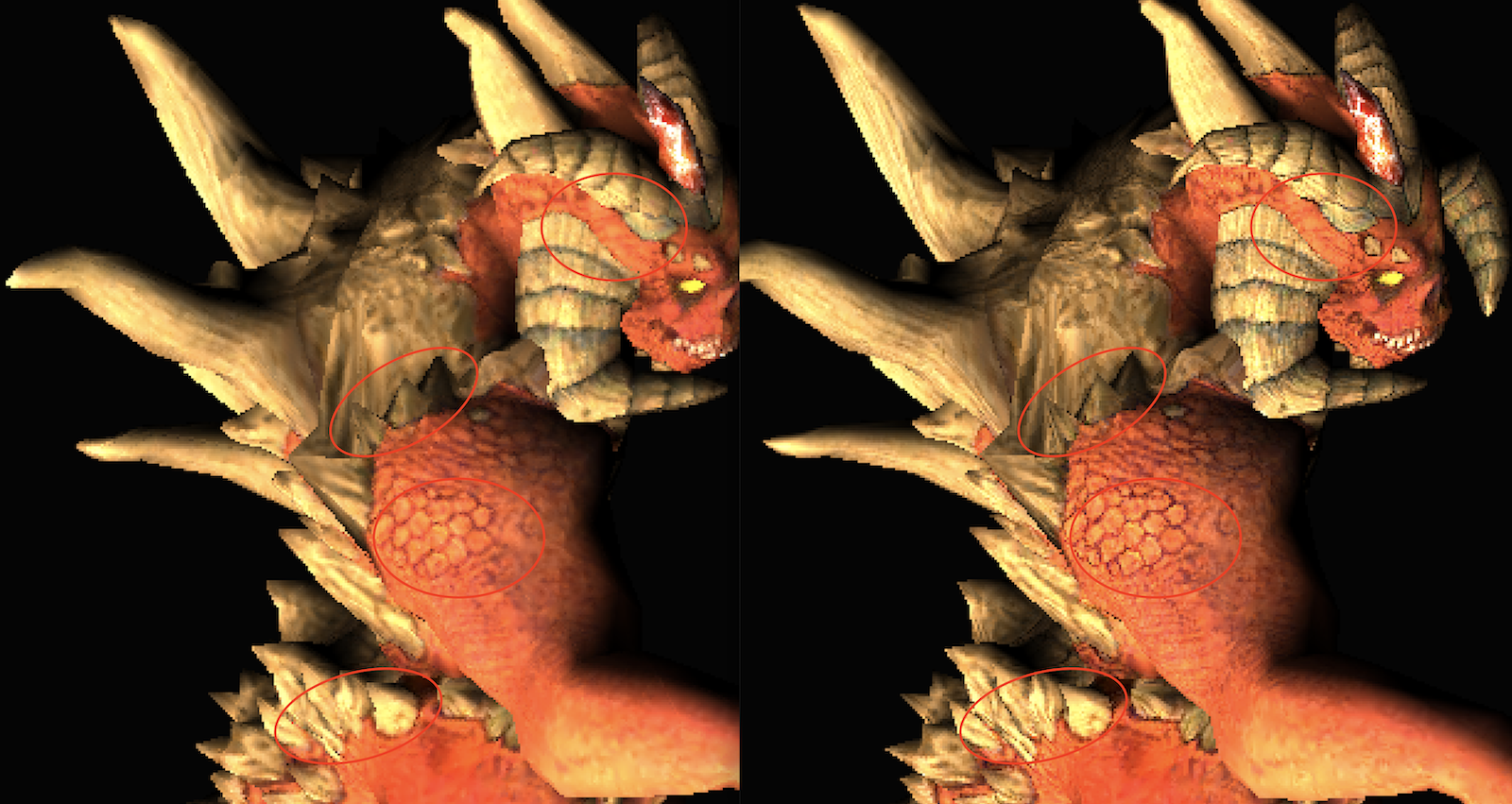
效果相对明显了,但我发现除了颜色变换剧烈的边缘,一些较为平滑的局部也被MSAA处理得糊成一片。原因是我们的策略会对一切sample hit数不为0的像素进行算术平均处理,这与MSAA的理念相违背了。
改进
若像素的sample hit数为4,则表明该像素并不处于三角形面片边缘,也就没必要进行MSAA平均处理,直接用改像素点本身的颜色着色就行了。有了这个觉悟,为代码加一段判定:
for 像素(x,y) in 当前三角形包围盒 {
.......
else if hit == 4.0 {
let 像素重心坐标 = barycentric(三角形三顶点,像素.x,像素.y);
let 深度 = 深度插值(像素重心坐标,三角形三顶点);
if 深度缓存(像素.x,像素.y)>深度 {
continue;
}
深度缓存(像素x, 像素.y, 深度);
帧缓存(像素.x, 像素.y, 着色器.颜色(像素重心坐标));
continue;
}
......
}
看看效果:
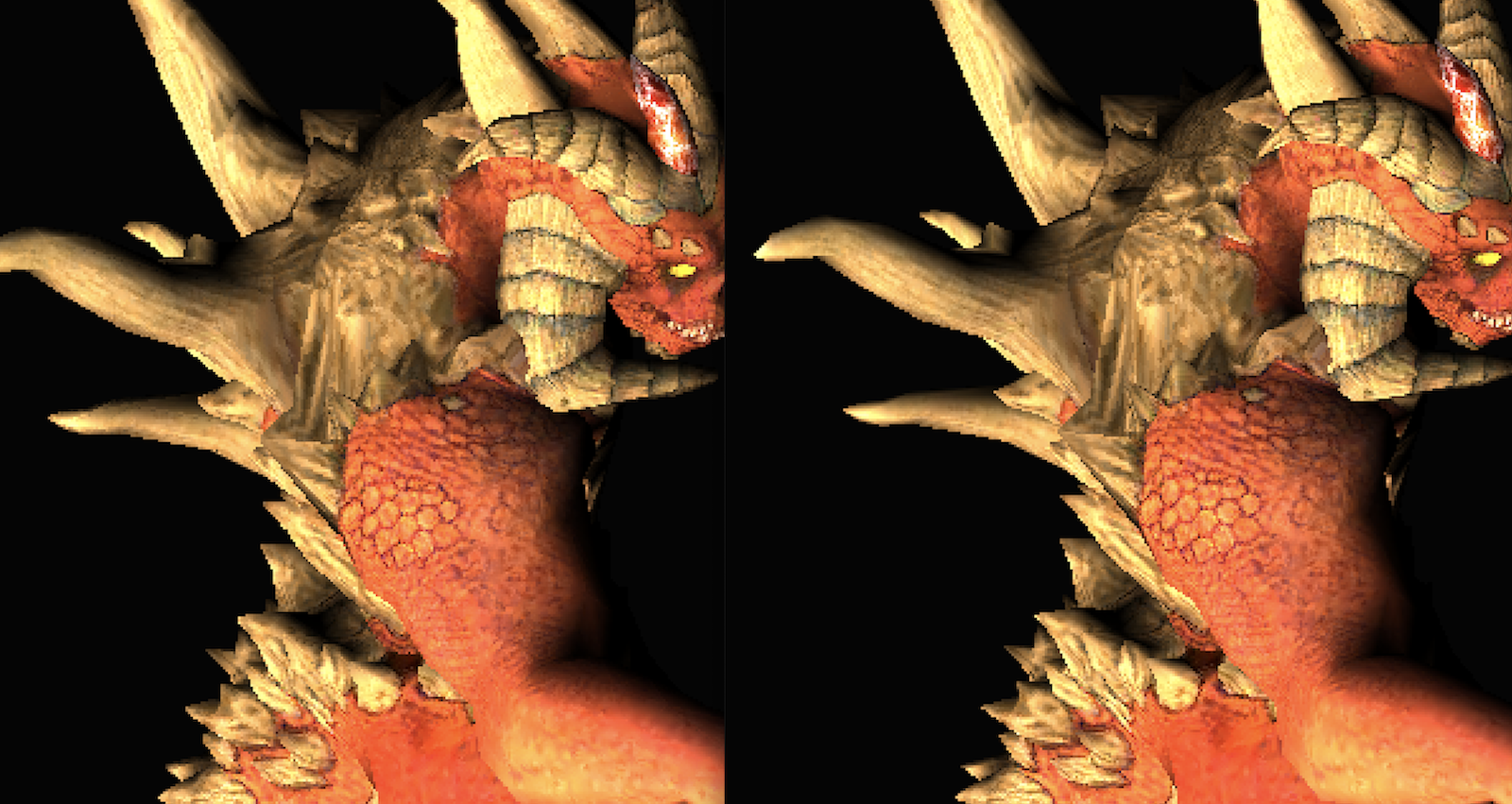
很明显内部平滑部分未被MSAA影响,但似乎对比起来效果不显著,这里我还是感到比较困惑,欢迎伙伴一起讨论。