Image Is Everything UVALive

VJ 传送门

题意：给你一个边长为n的正方体的六个面的颜色分布（每个面能看到的颜色） 其中有些正方体缺失， 问具体正方体的重量为（实际存在的单位正方体个数）

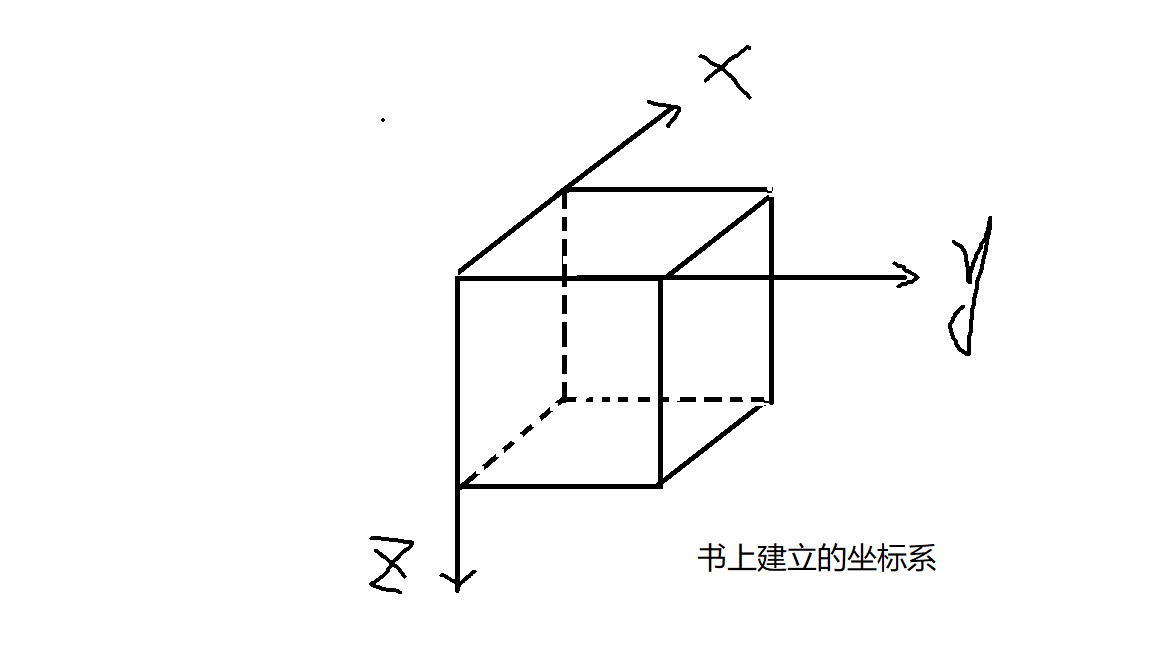
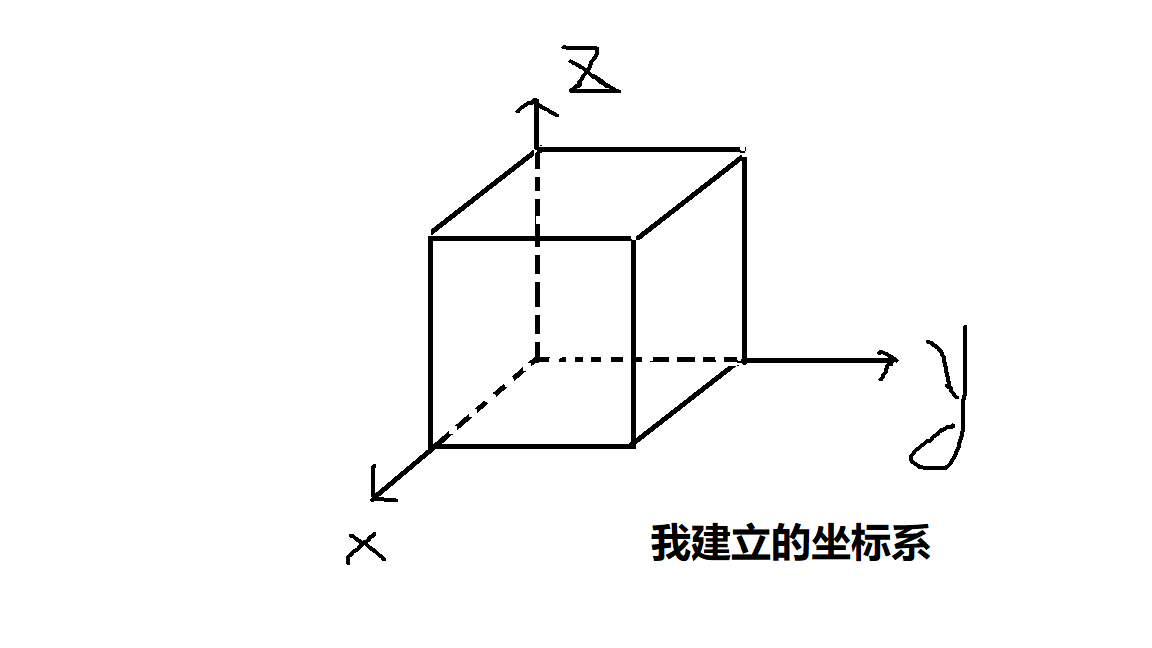
这道题蛮考验想象力的，开始想了半天 有想法但是写不出来  看了书上的解法觉得可以 大致做法就是先读入数据， 然后用一个三维数组表示这个正方体的所有单位正方体 然后每次将某个视图的某点投射到正方体里面， 每个点都能投射成n个点 （每个面上的点在空间上还有深度）， 然后每次当遇见 . 代表空心能够直接看穿的时候就删除这个点代表的所有正方体， 当这个点的其他视图颜色不一样时 也删除 直到没有不需要删除正方体为止（有些正方体的上一个是空的 但下一个还有 这个有点难说清 需要想象一下）， 书上建立的坐标系 和 我建立的坐标系如下图所示，

 简而言之就是把各个视图对应的正方体颜色进行比较 不相同就删掉 直到没有需要删去的正方体， 然后记录一下个数 即可

  在具体视图的点投射到空间里的时候 可以想象正方体翻转到当前这个视图这个面 这样的话 行和列的空间坐标会更好描述一点

   一个存在的单位正方体的六个视图的颜色都必定是相同的，否则不存在，将每个视图的每个视点投射到正方体的单位正方体中，然后如果某个单位正方体的某个视图颜色不相同，就把这个单位正方体给删去

 

#include<bits/stdc++.h>

using namespace std;
#define ll long long
#define _for(i,a,b) for(int i = (a); i < (b); i++)
#define _rep(i,a,b) for(int i = (a); i <= (b); i++)
#define all(v) (v).begin(), (v).end()

const int N = 15;
char pos[N][N][N], view[6][N][N];
int n;

void get(int i, int j, int k, int p, int& x, int& y, int& z) {//我建立的坐标系
    if(k == 0)      { x = n-p-1, y = j, z = n-i-1;} //   front
    else if(k == 1) { x = j, y = p, z = n-i-1;} //left
    else if(k == 2) { x = p, y = n-j-1, z = n-1-i;} //back
    else if(k == 3) { x = n-1-j, y = n-p-1, z = n-1-i;} //right
    else if(k == 4) { x = i, y = j, z = n-p-1; }  //top
    else            { x = n-1-i, y = j, z = p;}   //bottom
    return;
}
void get1(int i, int j, int k, int p, int& x, int& y, int& z) { //书上建立的
    if(k == 0)      { x = p, y = j, z = i;} //front
    else if(k == 1) { x = n-1-j, y = p, z = i;} //left
    else if(k == 2) { x = n-1-p, y = n-j-1, z = i;} //back
    else if(k == 3) { x = j, y = n-p-1, z = i;} //right
    else if(k == 4) { x = n-1-i, y = j, z = p; }  //top
    else            { x = i, y = j, z = n-1-p;}   //bottom
    return;
}
void task2995() {
    while(cin >> n and n) {
        _for(i,0,n) _for(k,0,6) {
            string s; cin >> s;
            _for(j,0,n) view[k][i][j] = s[j];
            //cout << s << " ";
        }// cout << "

";
        //_for(i,0,n) { _for(j,0,6) {   _for(k,0,n) cout << view[j][i][k]; cout << " ";}  cout << "
";}
        _for(k,0,n) _for(i,0,n) _for(j,0,n) pos[k][i][j] = '#';
        _for(k,0,6) _for(i,0,n) _for(j,0,n) 
        if(view[k][i][j] == '.')
            _for(p,0,n) {
                int x,y,z;
                get(i,j,k,p,x,y,z);
                pos[x][y][z] = '.';
            }
        
        for(;;) {
            bool done = true;
            _for(k,0,6) _for(i,0,n) _for(j,0,n) 
            if(view[k][i][j] != '.') _for(p,0,n) {
                int x,y,z;
                get(i,j,k,p,x,y,z);
                if(pos[x][y][z] == '.') continue;
                if(pos[x][y][z] == '#') {
                    //if(view[k][i][j] == '.')    done = false;
                    pos[x][y][z] = view[k][i][j];
                    break;
                }
                if(view[k][i][j] == pos[x][y][z]) break; //当颜色相同， 不用往下比较颜色了
                pos[x][y][z] = '.', done = false;
            }
            if(done) break;
        }
        int ans = 0;
        _for(i,0,n) _for(j,0,n) _for(k,0,n) if(pos[i][j][k] != '.') ans++;
        cout << "Maximum weight: " << ans << " gram(s)
";
    } return;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr);
    task2995();
    //task11464();
    //task3();
    return 0;
}