多项式拟合

来源：同登科 《计算方法》 中国石油大学出版社 P106

  *何为拟合？

　 从给定的函数表出发，寻找一个简单合理的函数近似表达式来拟合给定的一组数据。

   这里所说的“拟合”,即不要所作的曲线完全通过所有的Σ数据点，只要求所得的近似曲线能反映数据的基本趋势。数据拟合在实际中有广泛的应用。

   它的实质是离散情况下的最小平方趋近，基本思想和处理方法也具有相似性。其几何解释是：求一条曲线，使数据点均在离此曲线的上方或下方不远处。

 *多项式拟合

　　设由实验测得函数y=f(x)在n个点x₁ ,x₂,...,x_n的值为y₁,y₂,...,y_n,要求这个函数的一个近似表达式。我们用一个次数低于n-1(m<n-1)的多项式φ_m(x)来拟合它，设

　　　　　　　　　　　　　　　　φ_m(x) = a₀+a₁x+a₂x²+…+a_mx^m        (m < n -1)        　　　　　　　　　　　    　(1)

　　用最小二乘来确定系数a₀，a_1，…，a_m，令

　　　　　　　　　　　　　　　　Q(a₀,a₁,...,a_m)  = ∑ⁿ_i=1(φ_m(x)-y_i)²

　　　　　　　　　　　　　　　　　　　　　　 = ∑ⁿ_i=1(a0+a₁x_i+a₂x²_i+...+a_mx^m_i-y_i)²

　　选a₀,a₁,...,a_m，使Q(a₀,a₁,...,a_m)达到最小，将Q对a_k求偏导数，并令其等于零，有

                  

    或

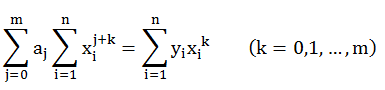　　　　　　　　　　        　　　　　　　　　　　　　　　    　（2）

   写成矩阵形式为

          　　　　　  （3）

   上述方程组就称为多项式拟合的正规方程组，其系数阵为一对称矩阵，计算时只须将下列一些和式求出即可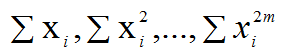：。若（3）式的系数行列式不等于零，则由（3）式可以唯一地确定系数a₀,a₁,...,a_m.

---

例  已知函数表如下

xi	1	3	4	5	6	7	8	9	10
yi	2	7	8	10	11	11	10	9	8

   试用二次多项式曲线来拟合这组数据。

解： 设二次多项式为φ(x) = a₀+a₁x+a₂x²,为了得到正规方程组，必须先算出以下各和：

　　　　　　　　　　　　

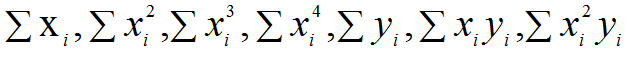
列表如下：

　　　　　　　　　　　　

由上表得正规方程组为

　　　　　　　　          

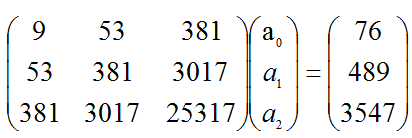
求解得  a₀=-1.4597,a₁=3.605,a₂=-0.2676,

    故φ(x)=-1.4597+3.6053x-0.2676x².