1.事件间的关系与运算
事件是一个集合,所以事件之间的关系与运算可以按照集合论中集合之间的关系与运算来处理.
设Ω为试验 E的样本空间, A , B , Ak ( k =1, 2,…)是试验E的随机事件,也是Ω的子集.
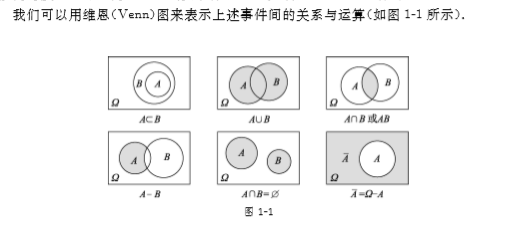
( 1)若A ⊂ B ,则称事件B包含事件A ,这指的是事件A的发生必然会导致事件B发生.
( 2)若A ⊂ B且 B ⊂ A ,即A = B ,则称事件A与事件 B相等.
( 3)事件A ∪ B ={ x | x ∈ A或 x ∈ B }称为事件A与事件B的和事件,当且仅当A , B中至少有一个事件发生时,事件A ∪ B发生.
类似地,称∪ n k =1 Ak为n个 事 件A 1, A 2,…, An的 和 事 件,称 ∪ ∞ k =1 Ak为 可 列 个 事 件A 1, A 2,…的和事件.
( 4)事件 A ∩ B ={ x | x ∈ A且 x ∈ B }称为事件A与事件B的积事件,当且仅当事件A , B都发生时,事件A ∩ B发生. A ∩ B也记作AB .
类似地,称∩ n k =1 Ak为n个 事 件A 1, A 2,…, An的 积 事 件,称 ∩ ∞ k =1 Ak为 可 列 个 事 件A 1, A 2,…的积事件.
( 5)事件 A B ={ x | x ∈ A且 x ∉ B }称为事件A与事件 B的差事件,当且仅当事件A发生, B不发生时,事件A B发生.
( 6)若A ∪ B = Ω且 A ∩ B =⌀,则称事件A与事件 B互为对立事件,又称事件A与事件B互为逆事件.这是指在每一次随机试验中,事件A
与事件 B必有一个事件且仅有一个事件发生. 事件 A的对立事件记为A ,易知A = Ω A , A ∪ A = Ω且A ∩ A =⌀.
( 7)若A ∩ B =⌀,则称事件A与事件 B互不相容(或互斥).这指的是事件A与事件 B不能同时发生,显然,同一随机试验中各个基本事件是两两互不相容的.
@在进行事件的运算时,经常要用到下述运算规律:设A , B , C为事件,则有
( 1)交换律: A ∪ B = B ∪ A , A ∩ B = B ∩ A ;
( 2)结合律:( A ∪ B )∪ C = A ∪( B ∪ C )= A ∪ B ∪ C , ( A ∩ B )∩ C = A ∩( B ∩ C )= A ∩ B ∩ C ;
( 3)分配律: A ∩( B ∪ C )=( A ∩ B )∪( A ∩ C ), A ∪( B ∩ C )=( A ∪ B )∩( A ∪ C );
( 4)自反律: A == A ;
( 5)对偶律: A ∪ B = A ∩ B , A ∩ B = A ∪ B