简介Floyd算法

目录

• 1. 定义
• 2. 优缺点
• 3. 基本思想
• 4. 算法过程示例
• 5. 小结

1. 定义

Floyd算法是一种用于寻找给定的加权图中顶点间最短路径，是经典的多源最短路径算法，可以有效地处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。

Floyd算法的时间复杂度为 (O(N^3))，空间复杂度为 (O(N^2))。

2. 优缺点

• 优点：
  容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。

• 缺点：
  时间复杂度比较高，不是和计算大量数据。

3. 基本思想

Floyd算法属于动态规划算法，即寻找节点 (i) 到节点 (j) 的最短路径。

Step 1: 初始距离
定义 (n) 节点网络的邻接矩阵 (A_{n imes n}) ，矩阵中的元素为 (a_{i,j}) 为节点 (i) 到节点 (j) 的一步的直线距离。令 (A^{(0)}=A)，其初始元素为 (a_{i,j}^{(0)})
则该距离有如下三种情况：

[a_{i,j}^{(0)}= egin{cases} c_{i,j}, i,j相连 \ 0, i=j \ infty, i,j不相连 end{cases} ]

其中，节点 (i, j) 之间有直线连接时，则 (a_{i,j}^{(0)}) 为其距离值 (c_{i,j})；节点 (i) 到自身的距离为 (0)；节点 (i, j) 之间没有直线连接时，则 (a_{i,j}^{(0)}) 则为 (infty)，如下图：

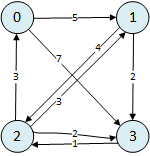
则该初始邻接矩阵 (A)为：

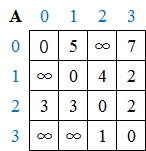
即节点0与节点0自身距离值为0，即 (A[0][0]=0)；
节点0与节点1之间有直线连接，距离值为5，即 (A[0][1]=5)；
节点0与节点2之间没有直线连接，则距离值为 (infty)，即 (A[0][2]=infty)；
节点0与节点3之间有直线连接，距离值为7，即 (A[0][3]=7) ……
其他节点间的初始距离可依次写出，即为该邻接矩阵 (A)。

Step 2: 借中转节点迭代找最短路径
节点 (i, j) 间一步达不到时，则需要在两节点之间通过其他节点（如节点 (k)）作连接：
在 (A) 矩阵上做 (n) 次迭代，(k=1,cdots,n)，第 (k) 次迭代

[a_{i,j}^{k}=min(a_{i,j}^{k-1},a_{i,k}^{k-1}+a_{k,j}^{k-1}) ]

即在节点 (i) 和节点 (j) 之间找到一条最短距离的路径，如下图：

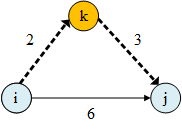
图中的节点 (i) 到节点 (j)之间的直线距离 ((i ightarrow j)) 为 (6)，但经过节点 (k) 作中转后，节点 (i) 到节点 (j)之间的直线距离 ((i ightarrow k ightarrow j)) 为 (2+3=5)，因此 (a_{i,j}^{k}=min(6,5)=5)。
运算过程中的 (k) 从 (1) 开始，而节点 (i, j) 则分别从 (1) 到 (n) 遍历所有的值，然后 (k) 加1，直到 (k) 等于 (n) 时停止。

Step 3: 得到所有节点的最短路径
遍历所有的节点，最后得到矩阵 (A)，其中 (a_{i,j}) 便存储了任意节点 (i) 到节点 (j) 顶点的最短路径的距离。

4. 算法过程示例

基于上述的基本思想，定义两个二维矩阵：

邻接矩阵 A 记录节点间的最短距离
      例如：A[0][3]=10，即表示节点 0 与节点 3 之间最短距离为10 

路径矩阵 P 记录节点间最短路径中的中转节点 
      例如：P[0][3]=1，即表示节点 0 与节点 3 之间的最短路径轨迹为：(0→1→3)

采用上面的节点图
Step 1: 初始的邻接矩阵 (A) 和路径矩阵 (P) 分别为：

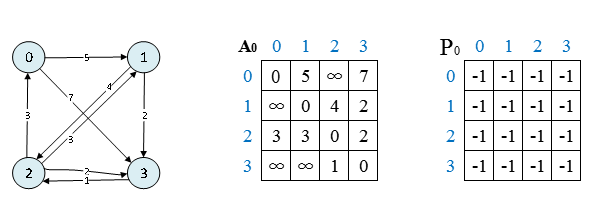
路径矩阵 (P) 还未开始查找，默认为 (-1)

Step 2: 开始迭代
T1: 节点 (0) 做中转节点：

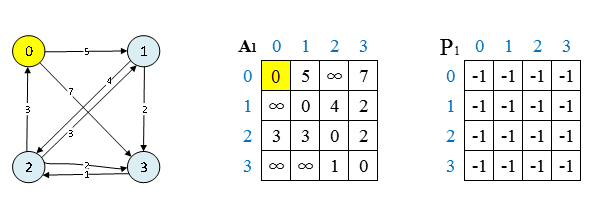
过程：
节点 (1) 到节点 (2)：{1,2}：比较 (A[1][2]>(A[1][0]+A[0][2]) ? ightarrow 4>(infty +infty) ? ightarrow A[1][2]=4) 不变
节点 (1) 到节点 (3)：{1,3}：比较 (A[1][3]>(A[1][0]+A[0][3]) ? ightarrow 2>(infty +7) ? ightarrow A[1][2]=2) 不变
节点 (2) 到节点 (1)：{2,1}：比较 (A[2][1]>(A[2][0]+A[0][1]) ? ightarrow 3>(3 +5) ? ightarrow A[1][2]=3) 不变
节点 (2) 到节点 (3)：{2,3}：比较 (A[2][3]>(A[2][0]+A[0][3]) ? ightarrow 2>(3 +7) ? ightarrow A[1][2]=2) 不变
节点 (3) 到节点 (1)：{3,1}：比较 (A[3][1]>(A[3][0]+A[0][1]) ? ightarrow infty>(infty +5) ? ightarrow A[3][1]=infty) 不变
节点 (3) 到节点 (2)：{3,2}：比较 (A[3][2]>(A[3][0]+A[0][2]) ? ightarrow 1>(infty +infty) ? ightarrow A[3][2]=1) 不变

T2: 节点 (1) 做中转节点：

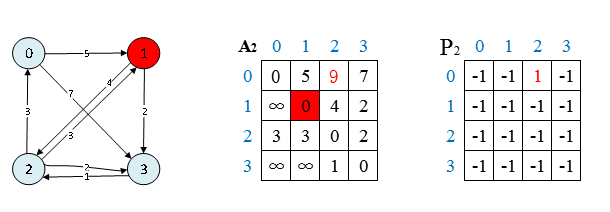
过程：
节点 (0) 到节点 (2)：{0,2}：比较 (A[0][2]>(A[0][1]+A[1][2]) ? ightarrow 9>(5 +4) ? ightarrow A[0][2]=9) 更改：经过节点 (1)
节点 (0) 到节点 (3)：{0,3}：比较 (A[0][3]>(A[0][1]+A[1][3]) ? ightarrow 7>(5 +2) ? ightarrow A[0][3]=7) 不变
节点 (2) 到节点 (0)：{2,0}：比较 (A[2][0]>(A[2][1]+A[1][0]) ? ightarrow 3>(3 +infty) ? ightarrow A[2][0]=3) 不变
节点 (2) 到节点 (3)：{2,3}：比较 (A[2][3]>(A[2][1]+A[1][3]) ? ightarrow 2>(3 +2) ? ightarrow A[2][3]=2) 不变
节点 (3) 到节点 (0)：{3,0}：比较 (A[3][0]>(A[3][1]+A[1][0]) ? ightarrow infty>(infty +infty) ? ightarrow A[3][0]=infty) 不变
节点 (3) 到节点 (2)：{3,2}：比较 (A[3][2]>(A[3][1]+A[1][2]) ? ightarrow 1>(infty +4) ? ightarrow A[3][2]=1) 不变

T3: 节点 (2) 做中转节点：

过程：
节点 (0) 到节点 (1)：{0,1}：比较 (A[0][1]>(A[0][2]+A[2][1]) ? ightarrow 5>(9 +3) ? ightarrow A[0][1]=5) 不变
节点 (0) 到节点 (3)：{0,3}：比较 (A[0][3]>(A[0][2]+A[2][3]) ? ightarrow 7>(9 +2) ? ightarrow A[0][3]=7) 不变
节点 (1) 到节点 (0)：{1,0}：比较 (A[1][0]>(A[1][2]+A[2][0]) ? ightarrow infty>(4 +3) ? ightarrow A[1][0]=7) 改变：经过节点 (2)
节点 (1) 到节点 (3)：{1,3}：比较 (A[1][3]>(A[1][2]+A[2][3]) ? ightarrow 2>(4 +2) ? ightarrow A[1][3]=2) 不变
节点 (3) 到节点 (0)：{3,0}：比较 (A[3][0]>(A[3][2]+A[2][0]) ? ightarrow infty>(1 +3) ? ightarrow A[3][0]=4) 改变：经过节点 (2)
节点 (3) 到节点 (1)：{3,1}：比较 (A[3][1]>(A[3][2]+A[2][1]) ? ightarrow infty>(1+3) ? ightarrow A[3][1]=4) 改变：经过节点 (2)

T4: 节点 (3) 做中转节点：

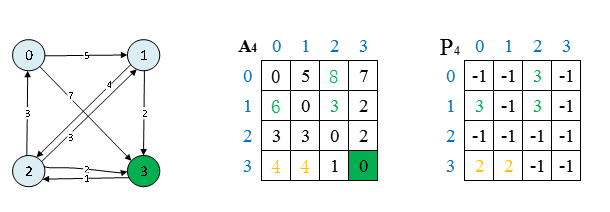
过程：
节点 (0) 到节点 (1)：{0,1}：比较 (A[0][1]>(A[0][3]+A[3][1]) ? ightarrow 5>(9 +4) ? ightarrow A[0][1]=5) 不变
节点 (0) 到节点 (2)：{0,2}：比较 (A[0][2]>(A[0][3]+A[3][2]) ? ightarrow 9>(7 +1) ? ightarrow A[0][2]=8) 改变：经过节点 (3)
节点 (1) 到节点 (0)：{1,0}：比较 (A[1][0]>(A[1][3]+A[3][0]) ? ightarrow 7>(2 +4) ? ightarrow A[1][0]=6) 改变：经过节点 (3)
节点 (1) 到节点 (2)：{1,2}：比较 (A[1][2]>(A[1][3]+A[3][2]) ? ightarrow 4>(2 +1) ? ightarrow A[1][2]=3) 改变：经过节点 (3)
节点 (2) 到节点 (0)：{2,0}：比较 (A[2][0]>(A[2][3]+A[3][0]) ? ightarrow 3>(2 +4) ? ightarrow A[2][0]=3) 不变
节点 (2) 到节点 (1)：{2,1}：比较 (A[2][1]>(A[2][3]+A[3][1]) ? ightarrow 3>(2+4) ? ightarrow A[2][1]=3) 不变

Step 3: 得到所有节点的最短路径
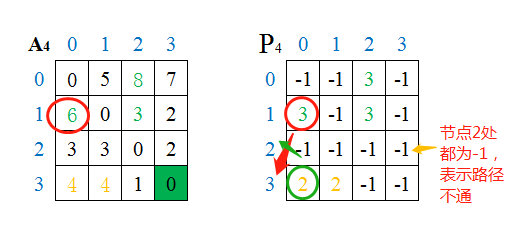
最终的邻接矩阵 (A) 和路径矩阵 (P)为：

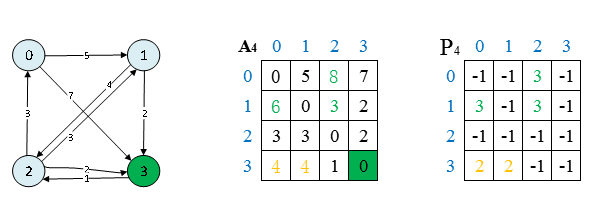
从上图可知：
从邻接矩阵 (A_4) 可知节点 (1) 到节点 (0) ((1 ightarrow 0))的最短路径距离为 (6)
从路径矩阵 (P_4) 可知节点 (1) 到节点 (0) ((1 ightarrow 0))的最短路径为 (1 ightarrow 3 ightarrow 2 ightarrow 0)

5. 小结

Floyd算法采用中转节点的方式，逐步对比得到各个路径的最短距离。