535 C.Tavas and karafs

C. Tavas and Karafs

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Karafs is some kind of vegetable in shape of an 1 × h rectangle. Tavaspolis people love Karafs and they use Karafs in almost any kind of food. Tavas, himself, is crazy about Karafs.

Each Karafs has a positive integer height. Tavas has an infinite 1-based sequence of Karafses. The height of the i-th Karafs is si = A + (i - 1) × B.

For a given m, let's define an m-bite operation as decreasing the height of at most m distinct not eaten Karafses by 1. Karafs is considered as eaten when its height becomes zero.

Now SaDDas asks you n queries. In each query he gives you numbers l, t and m and you should find the largest number r such that l ≤ r and sequence sl, sl + 1, ..., sr can be eaten by performing m-bite no more than t times or print -1 if there is no such number r.

Input

The first line of input contains three integers A, B and n (1 ≤ A, B ≤ 106, 1 ≤ n ≤ 105).

Next n lines contain information about queries. i-th line contains integers l, t, m (1 ≤ l, t, m ≤ 106) for i-th query.

Output

For each query, print its answer in a single line.

Sample test(s)

input

2 1 4
1 5 3
3 3 10
7 10 2
6 4 8

output

4
-1
8
-1

input

1 5 2
1 5 10
2 7 4

output

1
2

题读了好几遍才读懂。
题意是给出一个等差数列，操作严格要求从最左边不为零的连续m个数减去1，最多执行t次后问离最左边最远的位置在哪里。
有两个限制条件...一个是本身的si不能大于t，否则无法吃完。
还有一个是从sl到sr的和不能超过m*t (比赛的时候考虑的不周到。。实际上只有当r-l+1比m大的时候才是m，也就是说要取min(m,l-r+1))
这题正解应该是二分....直接Lower_bound。。。看到也有人用前缀和搞的。
我是解方程了（貌似是个傻逼做法）....
可以列出一个关于r的一元二次方程。。。然后求根公式2333
方程是： 

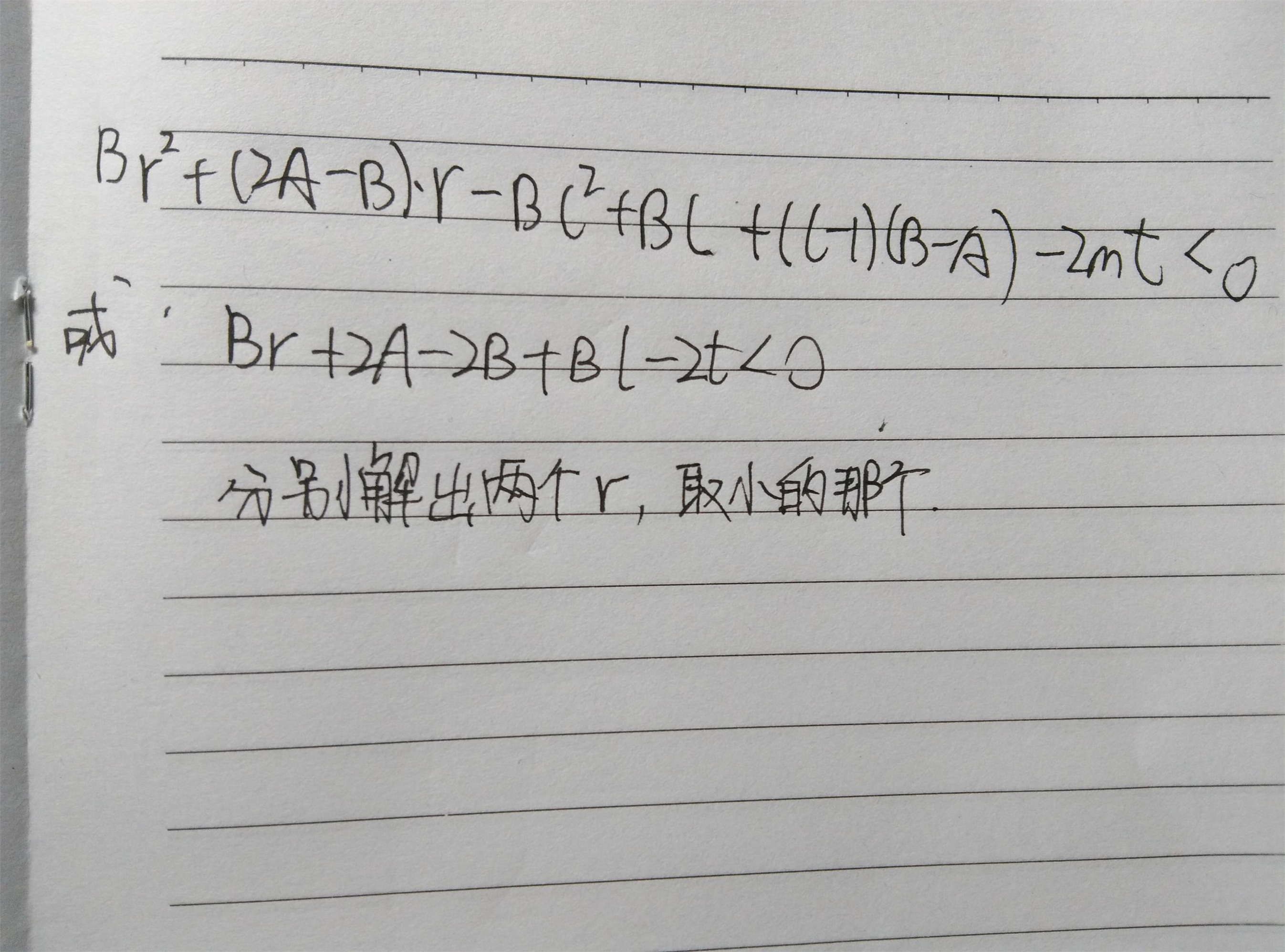
然后再和第一个条件得到的r比较取小的就是结果.....

等周末把这题的二分解法也写一些。

下面是蒟蒻傻逼的数学方恒解法的代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdio>

using namespace std;
typedef long long LL;
const int N=1e5+5;
LL A,B,n,l,t,m,p,q,k,ans,a,b,c,dd,q2;
long double d,pp;
int main()
{
    cin>>A>>B>>n;
    for ( int i = 1; i <= n ; i++ )
    {
        cin>>l>>t>>m;
        if ( t<A+B*(l-1) )
        {
            cout<<-1<<endl;
            continue;
        }
     //   l = A + (l-1)*B; //wtf。。。这行代码是什么鬼...
        p = (int) ((t-A)/B);
        p++;
        a=B;
        b=(2*A-B);
        c=-B*l*l+3*B*l-2*m*t-2*A*l+2*A-2*B;
        d=(-b+sqrt(b*b-4*a*c))/(2*a);
        //cout<<"a:"<<a<<endl;
        //cout<<"b:"<<b<<endl;
        //cout<<"c:"<<c<<endl;
       // cout<<"d:"<<d<<endl;
        q = int (d);
        q2 = int((2*t-2*A+2*B-l*B)/B);
       // cout<<"q1:"<<q<<endl;
      //  cout<<"q2:"<<q2<<endl;
        q = min(q,q2);
       // cout<<"p:"<<p<<endl;
     //   cout<<"q"<<q<<endl;
        ans = min (p,q);
        cout<<ans<<endl;
    }
    return 0;
}