题意:
在一个射击游戏里面,游戏者可以选择地面上 ([1,X]) 的一个点射击,并且可以在这个点垂直向上射击最近的 (K) 个目标,每个目标有一个价值,价值等于它到地面的距离。游戏中有 (N) 个目标,每个目标从 (L) 到 (R),距离地面高度 (D)。每次射击一个目标可以得到目标价值大小的分数,每次射击以后目标不会消失。如果你前一次游戏得到的分数如果大于 (P),那么这次你得到的分数就翻倍。
数据范围:(1<=N, M ,X<=10^5, P<=10^9)
分析:
主席树。
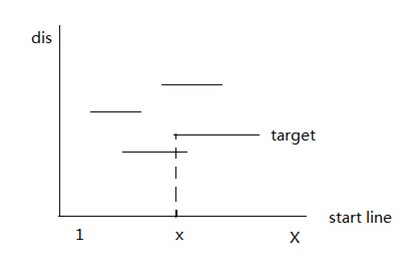
根据询问,可以发现是以地面坐标来进行询问的。因此,可以以地面坐标为时间轴,目标的高度为权值建立主席树。但由于询问的结果是可以射击到的目标的高度和,而不是查询区间第 (k) 小。因此,主席树要维护两个东西:1.每个高度的出现次数;2.区间的高度和。对于目标的范围,根据主席树前缀和的思想,在时间 (L) 相应的高度 (+1),在时间 (R+1) 相应的高度 (-1)。记录下每个时间点要进行的操作。
注意:当查询时,由于同一个高度的目标可能有多个,但查询可能不需要全部,所以要减掉一部分。
代码:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int,ll>P;
const int N=1e5+5;
int d[N];
vector<P>tar[N];
int root[N],cnt;
struct node
{
ll sum;
int num,lson,rson;
}sht[N*40];//N<<5会RE
int get_pos(int h,int len)
{
return lower_bound(d+1,d+1+len,h)-d;
}
int build(int l,int r)
{
int t=++cnt;
if(l==r)
{
sht[t].num=0;
sht[t].sum=0;
return t;
}
int mid=(l+r)>>1;
sht[t].lson=build(l,mid);
sht[t].rson=build(mid+1,r);
sht[t].sum=sht[sht[t].lson].sum+sht[sht[t].rson].sum;
sht[t].num=sht[sht[t].lson].num+sht[sht[t].rson].num;
return t;
}
int update(int l,int r,int pos,ll val,int rt)
{
int t=++cnt;
sht[t]=sht[rt];
if(l==r)
{
sht[t].num+=val;
sht[t].sum+=1LL*val*d[pos];
return t;
}
int mid=(l+r)>>1;
if(pos<=mid)
sht[t].lson=update(l,mid,pos,val,sht[rt].lson);
else
sht[t].rson=update(mid+1,r,pos,val,sht[rt].rson);
sht[t].sum=sht[sht[t].lson].sum+sht[sht[t].rson].sum;
sht[t].num=sht[sht[t].lson].num+sht[sht[t].rson].num;
return t;
}
P query(int l,int r,ll k,int rt)
{
if(l==r)
{
P tp=make_pair(l,sht[rt].num-k);
return tp;
}
int tn=sht[sht[rt].lson].num;
int mid=(l+r)>>1;
if(tn>=k)
return query(l,mid,k,sht[rt].lson);
else
return query(mid+1,r,k-tn,sht[rt].rson);
}
ll query2(int l,int r,int L,int R,int rt)
{
if(L<=l&&r<=R)
return sht[rt].sum;
int mid=(l+r)>>1;
ll ans=0;
if(L<=mid)
ans+=query2(l,mid,L,R,sht[rt].lson);
if(R>mid)
ans+=query2(mid+1,r,L,R,sht[rt].rson);
return ans;
}
int main()
{
int n,m,X,p,x,a,b,c;
while(scanf("%d%d%d%d",&n,&m,&X,&p)!=EOF)
{
int l,r,h;
cnt=0;
for(int i=0;i<=X+1;i++)
tar[i].clear();
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&l,&r,&h);
d[i]=h;
tar[l].pb(make_pair(h,1*1LL));
tar[r+1].pb(make_pair(h,-1*1LL));
}
sort(d+1,d+1+n);
int len=unique(d+1,d+1+n)-d-1;
int pos=1;
root[0]=build(1,len);
for(int i=1;i<=X;i++)
{
if(tar[i].size()==0)
{
root[i]=root[i-1];
continue;
}
for(int j=0;j<tar[i].size();j++)
{
P t=tar[i][j];
h=get_pos(t.first,len);
if(j==0)
root[i]=update(1,len,h,t.second,root[i-1]);
else
root[i]=update(1,len,h,t.second,root[i]);
}
}
ll pre=1;
while(m--)
{
scanf("%d%d%d%d",&x,&a,&b,&c);
ll k=(a*pre+b)%c;
P tp=query(1,len,k,root[x]);
ll ans=query2(1,len,1,tp.first,root[x]);
ans-=1LL*d[tp.first]*(max(tp.second,0*1LL));
if(pre>p)
ans*=2;
printf("%lld
",ans);
pre=ans;
}
}
return 0;
}