Query on A Tree
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 132768/132768 K (Java/Others)
Total Submission(s): 1732 Accepted Submission(s): 566
Problem Description
Monkey A lives on a tree, he always plays on this tree.
One day, monkey A learned about one of the bit-operations, xor. He was keen of this interesting operation and wanted to practise it at once.
Monkey A gave a value to each node on the tree. And he was curious about a problem.
The problem is how large the xor result of number x and one node value of label y can be, when giving you a non-negative integer x and a node label u indicates that node y is in the subtree whose root is u(y can be equal to u).
Can you help him?
Input
There are no more than 6 test cases.
For each test case there are two positive integers n and q, indicate that the tree has n nodes and you need to answer q queries.
Then two lines follow.
The first line contains n non-negative integers V1,V2,⋯,Vn, indicating the value of node i.
The second line contains n-1 non-negative integers F1,F2,⋯Fn−1, Fi means the father of node i+1.
And then q lines follow.
In the i-th line, there are two integers u and x, indicating that the node you pick should be in the subtree of u, and x has been described in the problem.
2≤n,q≤105
0≤Vi≤109
1≤Fi≤n, the root of the tree is node 1.
1≤u≤n,0≤x≤109
Output
For each query, just print an integer in a line indicating the largest result.
Sample Input
2 2 1 2 1 1 3 2 1
Sample Output
2 3
引:好久不写dfs序了,竟然忘了怎么写,正好借这个题熟悉一下。
我们先来弄明白dfs可以用来求什么。给你如下一棵树:
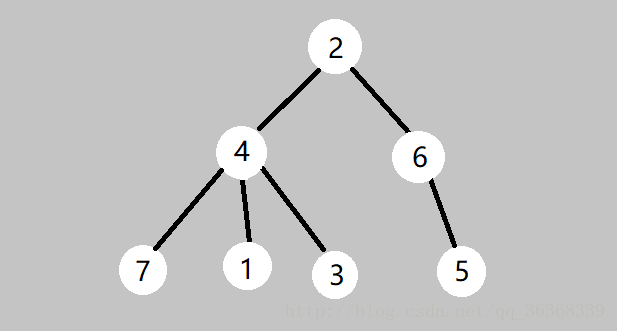
先上dfs序的代码:
1 void dfs(int x,int fa)
2 {
3 in[x]=++time;
4 num[time]=x;
5 for(int i=0;i<v[x].size();i++)
6 {
7 int to=v[x][i];
8 if(to==fa)
9 continue;
10 dfs(to,x);
11 }
12 out[x]=time;
13 }
其中in数组表示的是该节点第一次被访问到的时间,out数组表示的是遍历完该节点所有孩子后最后访问该节点的时间。num数组记录的是每个节点第一次被访问时的时间。对于上图,每个节点的信息如下:

所以假设我们想知道以4为根节点的子节点有哪些,就直接可以写
1 for(int i=in[4];i<=out[4];i++)
2 {
3 printf("%d
",num[i]);
4 }
本题题解:
先求出给出树的dfs序,然后遍历询问节点的子节点就好了。
1 #include<iostream>
2 #include<cstdio>
3 #include<cstring>
4 #include<vector>
5 #include<algorithm>
6 using namespace std;
7 const int maxn=1e5+10;
8 vector<int>v[maxn];
9 int val[maxn];
10 int in[maxn],out[maxn],num[maxn];
11 int n,q;
12 int time=0;
13 void dfs(int x,int fa)
14 {
15 in[x]=++time;
16 num[time]=x;
17 for(int i=0;i<v[x].size();i++)
18 {
19 int to=v[x][i];
20 if(to==fa)
21 continue;
22 dfs(to,x);
23 }
24 out[x]=time;
25 }
26 int main()
27 {
28 while(~scanf("%d%d",&n,&q))
29 {
30 time=0;
31 for(int i=1;i<=n;i++)
32 {
33 scanf("%d",&val[i]);
34 v[i].clear();
35 }
36 for(int i=2;i<=n;i++)
37 {
38 int x;
39 scanf("%d",&x);
40 v[x].push_back(i);
41 }
42 dfs(1,0);
43 while(q--)
44 {
45 int ans=0;
46 int u,x;
47 scanf("%d%d",&u,&x);
48 for(int i=in[u];i<=out[u];i++)
49 {
50 int tmp=x^val[num[i]];
51 if(tmp>ans)
52 ans=tmp;
53 }
54 printf("%d
",ans);
55 }
56 }
57 }