【编译原理】求First和Follow

写这篇博客的原因，是因为考试前以为自己已经将这个问题弄清楚了，但是，考试的时候，发现自己还是不会，特别是求follow集合。虽然考试结束了，希望可以帮助屏幕前的你，可以真正理解这个问题。

码字和做视频都不容易，可以给个三连吗？嗷呜~

2020-09-12更新第一版

2021-04-13更新第二版

2021-06-22更新第三版

讲解视频

博客对应的视频教程地址（一定要看看）：https://www.bilibili.com/video/BV17K4y1a72M#reply4409274160

视频中的一些问题

下面列举的问题可以先不看，等到视频看完，再拉到对应的时间点看视频中小小的错误

视频的05:12 剪辑视频的时候写错了,正确的应该是First(β) 
视频的07:11 忘记计算First(T)和Follow(T)，笔记中补了
视频的09:09 利用规则2或3两边可以是一样的非终结符
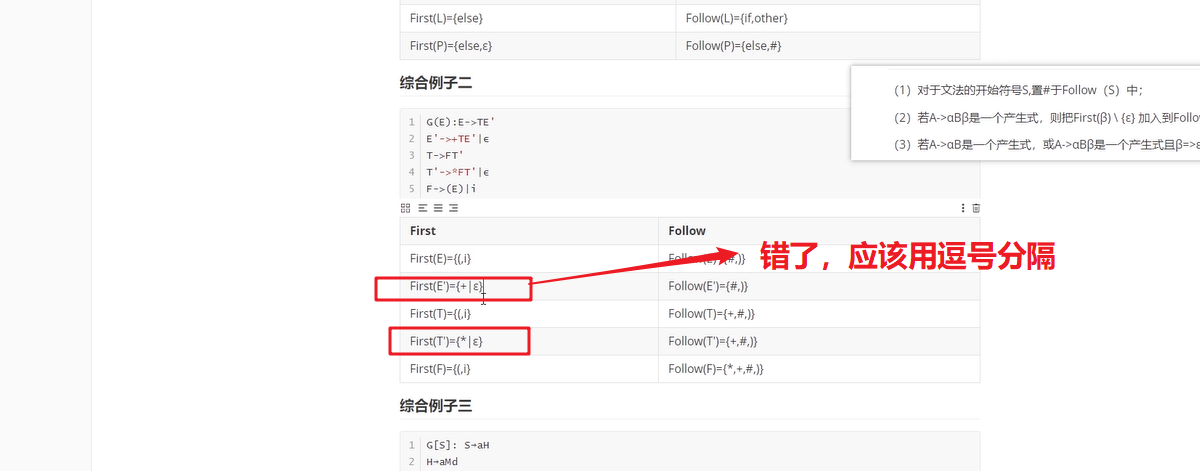
视频的12:03 First(E')和First(T')应该用逗号分隔

---

---

First集

官方定义

设G=(VT，VN，S，P)是上下文无关文法 ，则

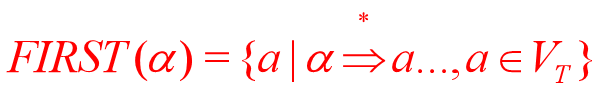
理解定义

不求信达雅，但求“说人话”。官方定义看不懂？下面的描述比较通俗易懂。

FIRST(A)是以A的开始符的集合，A的所有可能推导的开头终结符或者是ε

例子

通过例子来加强理解。

1. 后面跟的不是非终结符

...
A->aB|ε
A->c
...
First(A)={a，ε，c}

2. 后面跟非终结符（一）

...
A->Ba
B->b
...
First(A)={b}

3. 后面跟非终结符（二）

...
A->Bc
B->b|ε
...
First(A)={b,c}

4. 后面跟非终结符（三）

...
A->BC
B->b|ε
C->c|ε
...
First(A)={b,c,ε}

Follow集

相对于First集，Follow集的理解会稍微难一点，但是认真听，还是简单的。

官方定义

这个是信达雅版本的定义

假定S是文法G的开始符号，对于G的任何非终结符A,我们定义

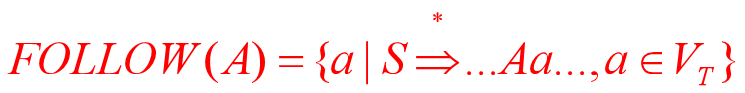
理解定义

这个是“说人话”版本的定义

Follow(A)为非终结符A后跟符号的集合,Follow(A)是所有句型中出现在紧接A之后的终结符或'#'

求解规则

（1）对于文法的开始符号S,置#于Follow（S）中；

（2）若A->αBβ是一个产生式，则把First(β) {ε} 加入到Follow（B）中

（3）若A->αB是一个产生式，或A->αBβ是一个产生式且β=>ε，则把Follow(A)加入到Follow(B)中

理解求解规则

（1）对于开始符号，首先将#放入Follow集中

（2）形如A->αBβ

（α可以是终结符或者非终结符或者直接为空，β可以是终结符或者非终结符，
注意β不能为空，B后面要有东西，
注意β不能为空，B后面要有东西，
注意β不能为空，B后面要有东西）

比如

A->aBC
A->aBd
A->BC
A->Bd

将First(β) {ε}（即First(β)除去ε） 加入到Follow（B）中

（3）形如A->αB(α可以是终结符或者非终结符或者直接为空)或者A->αBβ是一个产生式且β=>ε

比如

A->B
A->cB

A->dBC
C->ε

将Follow(A)加入到Follow(B)中

综合例子

让我们通过例子来对上面的知识点进行梳理和再次的理解。

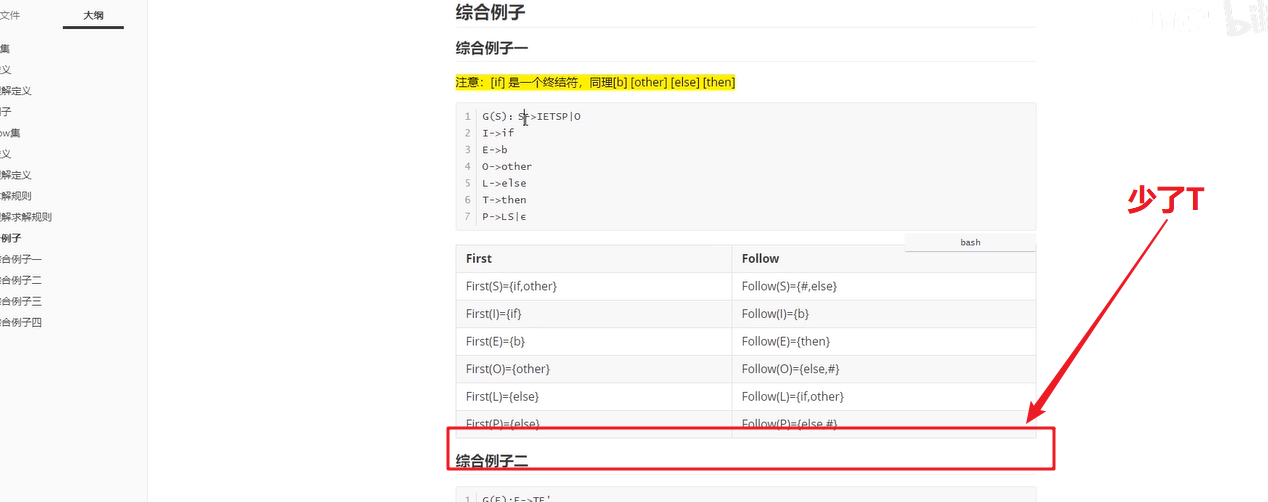
综合例子一

注意：[if] 是一个终结符，同理[b] [other] [else] [then]

G(S)：S->IETSP|O
I->if
E->b
O->other
L->else
T->then
P->LS|ε

First	Follow
First(S)={if,other}	Follow(S)={#,else}
First(I)={if}	Follow(I)={b}
First(E)={b}	Follow(E)={then}
First(O)={other}	Follow(O)={else,#}
First(L)={else}	Follow(L)={if,other}
First( P )={else,ε}	Follow( P )={else,#}
First(T)={then}	Follow(T)={if,other}

综合例子一 中反馈的问题：

• S->IETSP|O 中求Follow(S)能运用规则2和3来求解S吗？

解答：

可以的，虽然规则中给出的是A和B两个不同的非终结符，但是
A和B在实际运用的过程中是可以相等的，即B=A
A和B在实际运用的过程中是可以相等的，即B=A
A和B在实际运用的过程中是可以相等的，即B=A
S->IETSP|O S后面有P,利用规则3，将First(P)加入Follow(S)中
但是，发现P可以等于ε，即S->IETS，利用规则二，将Follow(S)加入Follow(S)中

• 在求Follow(S)发现P->LS|ε也是存在的，那么follow(s)={#,else}+follow( p )，而算到follow( p )发现follow( p )=follow(s) 就不知道怎么算了

解答：（很重要，认认真真地看）

我们需要同时满足
follow(s)={#,else}+follow(p)
follow(p)=follow(s)
将第二个式子带入一式得到
follow(s)={#,else}+follow(s)
注意：不能将follow(s)约掉，而是要想怎么样上面的等式仍然成立
那么，我们就会发现follow(s)只能等于{#,else}
因为 {#,else}={#,else}+{#,else}是成立的

综合例子二

G(E):E->TE'
E'->+TE'|ε
T->FT'
T'->*FT'|ε
F->(E)|i

First	Follow
First(E)={(,i}	Follow(E)={#,)}
First(E')={+,ε}	Follow(E')={#,)}
First(T)={(,i}	Follow(T)={+,#,)}
First(T')={*,ε}	Follow(T')={+,#,)}
First(F)={(,i}	Follow(F)={*,+,#,)}

综合例子二 中反馈的问题：

• 为什么求E的FOLLOW集看到F->(E)|I直接将)右括号直接加入Follow中

解答：

这个问题需要回到最初的定义来理解
follow集的意思是紧跟后面的符号集，E后面有），即E后面有终结符。
属于规则二，但是终结符没有first和follow，所以直接添加即可。

综合例子三

G[S]: S→aH
H→aMd
H→d
M→Ab
M→ε
A→aM
A→e

First	Follow
First(S)={a}	Follow(S)={#}
First(H)={a,d}	Follow(H)={#}
First(M)={a,e,ε}	Follow(M)={d,b}
First(A)={a,e}	Follow(A)={b}

综合例子四

G(E):E->TE'
E'->+E|ε
T->FT'
T'->T|ε
F->PF'
F'->*F'|ε
P->(E)|a|b|^

First	Follow
First(E)={(,a,b,^}	Follow(E)={#,)}
First(E')={+,ε}	Follow(E')={#,)}
First(T)={(,a,b,^}	Follow(T)={+,#,)}
First(T')={(,a,b,^,ε}	Follow(T')={+,#,)}
First(F)={(,a,b,^}	Follow(F)={(,a,b,^,+,#,)}
First(F')={*,ε}	Follow(F')={(,a,b,^,+,#,)}
First( P )={(,a,b,^}	Follow( P )={*,(,a,b,^,+,#)}

综合例子四中反馈的问题：

怎么求follow(E)和follow(E‘)?

根据G(E)和规则一，#加入follow(E)
根据P->(E)|a|b|^和规则二，)加入follow(E)
根据E'->+E|ε和规则三，将follow（E'）到follow（E）里面

根据E->TE'和规则三得到将follow（E）到follow（E‘）里面 

=>
Follow(E)={#,)}+Follow(E')
Follow(E')=Follow(E)
根据综合例子一中一样的分析方法
Follow(E)={#,)}+Follow(E)=>Follow(E)={#,)}