题目大意:
给一个范围[1,n],从中找出两个数x,y,使得gcd(x,y)为质数,问有多少对(x,y有序)
解法:
不难,欧拉函数练手题,可以定义集合P ={x|x为素数},那么我们枚举gcd(x,y)可能等于的情况,对于任意p∈P可以得到:gcd(k1·p,k2·p) = p,当且仅当gcd(k1,k2) =1;那么我们就只需要枚举所有的k1,k2了。不妨设k1>k2,那么给定k1,k2的个数就是phi(k1),因为有序,所以给phi*2,但是,这样是否漏算了呢?没错,漏算了(1,1),补上就行了,那么这个的答案就是计算下面那个表达式。

稍有常识的人就会看出,如果我们的坦克再前进一步(大雾)要算这个式子,复杂度是O(n^2)的,我们分析一下复杂度主要消耗再哪里。
1.算phi
如果我们用暴力公式,也就是 的话,复杂度显然是很高的,全算出来高达(不是那个高达)O(n*sqrt(n)),这样的复杂度在1e7内是无法忍受的,所以我们
的话,复杂度显然是很高的,全算出来高达(不是那个高达)O(n*sqrt(n)),这样的复杂度在1e7内是无法忍受的,所以我们
必须另外想办法,下面我引入三个很厉害东西:
1.当p∈P时,phi(p) = p-1;
2.如果i mod p = 0, 那么 phi(i * p)=p * phi(i),证明略,其实我也不会证
3.若i mod p ≠0, 那么 phi( i * p )=phi(i) * ( p-1 ) ;
有了这三个就容易写出线性的求euler函数了。
2.二重循环
里面那一重循环可以在外面递推乱搞,自己想,或者看我代码。
那么这个的复杂度就降为了O(n);
3.下面是代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 int flag[10000001],p[6000000],tot; 4 int phi[10000001]; 5 void get_p(int end){ 6 for(int i=1;i<=end;i++) 7 flag[i] = 1; 8 for(int i=2; i<=end; i++){ 9 if(flag[i]==1){ 10 p[++tot]=i; 11 phi[i] = i-1; 12 } 13 for(int j=1; j<=tot && p[j]*i<=end; j++){ 14 flag[p[j]*i]=0; 15 if(i%p[j]==0){ 16 phi[i*p[j]] = p[j] * phi[i]; //欧拉函数的特性 17 break; 18 }else phi[i*p[j]] = (p[j]-1) * phi[i]; 19 } 20 } 21 } 22 long long f[10000001]; 23 24 int main(){ 25 int n; 26 cin >> n; 27 get_p(n); 28 f[1] = 1; 29 for(int i=2;i<=n;i++){ 30 f[i] = f[i-1] +phi[i]*2; 31 } 32 long long ans = 0; 33 for(int i=1;i<=tot;i++){ 34 ans = ans+f[n/p[i]]; 35 } 36 cout<<ans; 37 return 0; 38 }
4.拓展
这个问题就这么轻易的解决了,但是我们稍加思考,就能想到它的一个变式:
变式链接: bzoj2301
给一个范围[l,n],[p,m],定义x,y,x∈[1,n],y∈[1,m],使得gcd(x,y)=k,问有多少对(x,y无序)。
对于这道题,我们不得不引入新的概念,莫比乌斯反演:
其内涵主要是下面这个公式 ,其中mu是莫比乌斯函数,其定义为:
,其中mu是莫比乌斯函数,其定义为:
 ki表示x的唯一分解后每个质数的次数。µ函数还有一个性质
ki表示x的唯一分解后每个质数的次数。µ函数还有一个性质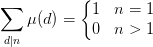
上面的莫比乌斯反演公式我们还有一种表达方法, 本题要用的就是这个。
本题要用的就是这个。
5.解决
可设f(x)表示gcd(a,b)=x的个数,F(x)表示满足x|gcd(a,b)的个数。那么我们可以考虑把区间分为两部分,对于[l,n],我们可以将它分为[1,n]-[1,l]+{l}(又不是搞数学那么讲究干嘛),然后我们先计算在[1,n]中有多少个a是x的倍数,容易得到这个数字为n/x。同理我们可以求得在[1,l]中有l/x个,在[1,m]中有m/x个,在[1,p]中有p/x个。这样我们就容易得到在[l,n]这个闭区间中有s1=(n/x-l/x+[l|x])注意,这里的[l|x]表示的是下面的意思。同样,我们也可以得到在[p,m]中有s2=(m/x-p/x+[p|x])。那么F(x) =s1*s2个(乘法原理)。
1 if(x % i == 0) 2 return 1; 3 else 4 return 0;
并且我们还能得到另一个式子 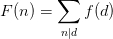 ,我们的目的是要求f(k),那么由这个式子和莫比乌斯反演公式可以得到,
,我们的目的是要求f(k),那么由这个式子和莫比乌斯反演公式可以得到,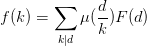 ,嗯,我写一下看看提交上去会不会超时哈。
,嗯,我写一下看看提交上去会不会超时哈。