({ t P1886}) 原题传送门
({ t P2032}) 原题传送门
({ t Solution})
这两道都是单调队列非常经典且模板的题目。
借此来浅析单调队列(Monotone queue)
概念
单调队列是一种特殊的队列,它在满足队列所有性质的同时,也满足以下特点 :
- 单调递增 (||) 单调递减 (||) 自定义的单调性
- 队首和队尾都可以出队,但只有队尾可以入队。
- 单调队列的队头一定是当前队列中的最值 ((max or min))
分析
单调队列的操作主要用到的是两个数组,作用如下 :
- 一个 (p[Maxn]) 数组,用来记录当前队中的元素
- 一个 (pos[Maxn]) 数组,用来记录当前队中的元素在初始序列中的下标
( ext{Example}:)
以此题样例为例 :
Input:
8 3
1 3 -1 -3 5 3 6 7
Output:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
模拟一下操作过程 : (以找最小值,单调递增的单调队列为例)
- (a[1](1)) 入队,(p={1} , pos={1})
- (a[2](3)) 入队,保持单调性,(p={1,3} , pos={1,2})
- (a[3](-1)) 入队,破坏了单调性,且 (-1<1<3),故 (1) 从队头出队,(3) 从队尾出队,(p={-1} , pos={3})
- (a[4](-3)) 入队,破坏了单调性,且 (-3<-1),故 (-1)从队尾出队,(p={-3} , pos={4})
- (a[5](5)) 入队,保持单调性,(p={-1,5} , pos={4,5})
- (a[6](3)) 入队,破坏了单调性,且 (3<5),但(-3<3),故 (5) 从队尾出队,(p={-3,3} , pos={4,6})
- (a[7](6)) 入队,保持单调性,(p={-3,3,6} , pos={4,6,7}),但样例中 (k=3),最多只能选长度 (3) 的窗口,故 (-3) 从队头出队,故应为(p={3,6} , pos={6,7})
- (a[8](7)) 入队,保持单调性,(p={3,6,7} , pos={6,7,8})
在上述过程中,除 (a[7]) 入队时出现了窗口长度的问题特别说明外,其余各元素进队时也应比较窗口长度,保证合法。
即题目描述中的这个过程 :
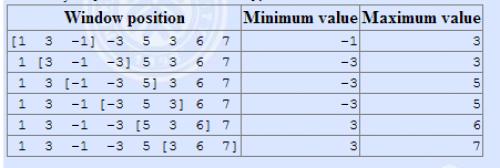
(从POJ搬来的实锤了)
所以说可以得到以下代码 :
inline void min(){
head=1;tail=0; //队头与队尾的指针
for(int i=1;i<=n;i++){ //i表示当前滑动窗口的右端点的下标
while(head<=tail && q[tail]>=a[i]) tail--; //求最小值,单调递增。
//故当队尾元素比当前入队元素大时,不满足"单调递增",队尾出队
q[++tail]=a[i]; //入队
pos[tail]=i; //记录位置
while(pos[head]<=i-k) head++; //i从1开始,i-k表示当前窗口的左端点的下标
//如果当前的窗口的长度无法到达队头,队头出队
if(i>=k) printf("%d ",q[head]); //至少能从1位置放下一个滑动窗口,即合法时输出队头(最小值)
}
printf("
");
}
这里可能有一个问题,为什么要
head=1;tail=0;
原因如下 :
(head) 要严格对应首元素, (tail) 要严格对应尾元素,因为是 (head<=tail) ,故当队列中加入一个元素时,(head=1,tail=0 o head=1,tail=1) 满足 (head<=tail) ,就可以表示有元素。
但是,这种赋值方法不一定,视具体题目而定
最大值同理(实际上只改了一个符号而已······)
({ t Code - P1886})
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
inline void read(int &x){
int f=1;
char ch=getchar();
x=0;
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
x*=f;
}
struct Monotone_queue{
int n,k;
int a[1000010];
int pos[1000010],q[1000010];
int head,tail;
inline void read_do(){
read(n);read(k);
for(int i=1;i<=n;i++) read(a[i]);
}
inline void min(){
head=1;tail=0;
for(int i=1;i<=n;i++){
while(head<=tail && q[tail]>=a[i]) tail--;
q[++tail]=a[i];
pos[tail]=i;
while(pos[head]<=i-k) head++;
if(i>=k) printf("%d ",q[head]);
}
printf("
");
}
inline void max(){
head=1;tail=0;
for(int i=1;i<=n;i++){
while(head<=tail && q[tail]<=a[i]) tail--;
q[++tail]=a[i];
pos[tail]=i;
while(pos[head]<=i-k) head++;
if(i>=k) printf("%d ",q[head]);
}
}
}m;
int main(){
m.read_do();
m.min();
m.max();
return 0;
}
({ t P2032}) 的代码基本相似,我们这里维护的是一个单调递减的单调队列。
({ t Code - P2032})
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int Maxn=2e6+10;
inline void read(int &x){
int f=1;
char ch=getchar();
x=0;
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+(ch&15);
ch=getchar();
}
x*=f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,k;
int a[Maxn];
int main(){
read(n);read(k);
for(int i=1;i<=n;i++) read(a[i]);
int q[Maxn],l=1,r=1;
for(int i=1;i<=n;i++){
while(l<=r&&q[l]<=i-k) l++;
while(l<=r&&a[q[r]]<=a[i]) r--;
q[++r]=i;
if(i>=k) write(a[q[l]]),putchar('
');
}
return 0;
}