T79167 新田忌赛马

题目链接

题目背景

田忌又要和齐王赛马了，这一次赛的不止三匹马，田忌请学OI的你帮忙

题目描述

田忌和齐王各有n匹马(1<=n<=1000)，他们的编号分别是1-n,给出田忌每条马能胜过齐王的哪些马（非赢则输，不存在平局的情况），每匹马最多出战一次，可以自由安排交战顺序，问田忌最多可以赢多少局。

输入输出格式

输入格式：

一行一个数n, 表示齐王和田忌各自马的数量 下面n行 第i行第一个数c，表示田忌的第i匹马能赢得马的数量，这一行后面有c个数,表示第i匹马能赢得对方的马的编号

输出格式：

一个数ans,表示田忌的最大胜场数

输入样例1：

4
3 2 1 3 
1 2 
2 2 1 
1 3 

输出样例1：

3

输入样例2：

8
1 6 
4 5 1 4 2 
4 3 1 6 5 
1 5 
1 2 
2 4 5 
6 3 1 4 2 7 6 
4 3 7 6 2 

输出样例2：

7

说明

对于20%的数据 n<=20 对于50%的数据 n<=200 对于100%的数据 n<=2000 c<=n

思路：

　　本题是二分图最大匹配：

　　1、匈牙利算法(只能拿90分， 被一个无良的出题人卡掉一个点)：

　　 　　核心思想：寻找增广路径，用增广路径求二分图最大匹配。

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstring>

using namespace std;

int n,a,b;
int line[2008][2008],use[2008],horse[10008];
int ans=0;

long long read()
{
    long long x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

int find(int x)//寻找增广路径 
{
    for(int i=1;i<=n;++i)//扫描右图每一个点 
    {
        if(line[x][i]&&!use[i])//如果x与i可以匹配，并且i没有被拆开尝试匹配并失败 
        {
            use[i]=1;//标记i在此轮中被拆开尝试匹配 
            if(horse[i]==0||find(horse[i]))//如果i没有被匹配过，或者现在i的匹配对象可以匹配到别人 
            {
                horse[i]=x;
                return 1;
            }
        }
    }
    return 0;
}

int main()
{
    n=read();
    for(int i=1;i<=n;++i)
    {
        a=read();
        for(int j=1;j<=a;++j)
        {
            b=read();
            line[i][b]=1;
        }
    }
    for(int i=1;i<=n;++i)
    {
        memset(use,0,sizeof(use));
        if(find(i)) ans++;//真就能找到一条增广路径，假则否 
    }
    printf("%d",ans);
    return 0;
}

　　2、网络流：

　　　　其实所有的二分图最大匹配问题都可以用网络流来做，并且比匈牙利算法更优。若对网络流有疑问可以看一下算法篇里的网络流。

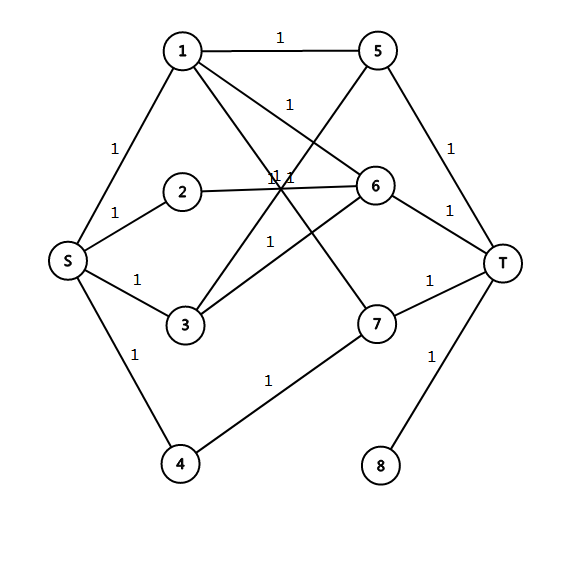
　　　　如样例1的数据，图应该是这样的。其中，ST分别为超级源点汇点。

　　

　　

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<iostream>

const int inf=0x7fffffff;

using namespace std;

int n,m,S,T;
int u,v,w;
int head[10008],num_edge=0;
int deep[10008];

struct Edge{
    int next,to,dis;
}edge[100008<<1];

queue <int> q;

long long read()
{
    long long x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

void addedge(int from,int to,int dis)
{
    edge[++num_edge].next=head[from];
    edge[num_edge].to=to;
    edge[num_edge].dis=dis;
    head[from]=num_edge;
}

bool bfs()
{
    memset(deep,0,sizeof(deep));
    while(!q.empty()) q.pop();
    deep[S]=1;
    q.push(S);
    do
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(deep[v]==0&&edge[i].dis)
            {
                deep[v]=deep[u]+1;
                q.push(v);
            }
        }
    }while(!q.empty());
    if(deep[T]!=0) return 1;
    else return 0;
}

int dfs(int u,int dist)
{
    if(u==T) return dist;
    for(int i=head[u];i;i=edge[i].next)
    {
        if( deep[edge[i].to]==deep[u]+1 && edge[i].dis!=0 )
        {
            int di=dfs(edge[i].to,min(dist,edge[i].dis));
            if(di>0)
            {
                edge[i].dis-=di;
                edge[i+1].dis+=di;
                return di;
            }
        }
    }
    return 0;
}

int xiongyali()
{
    int ans=0;
    while(bfs())
    {
        while(int di=dfs(S,inf))
        {
            ans+=di;
        }
    }
    return ans;
}

int main()
{
    n=read();m=n;S=10002;T=10003;
    for(int i=1;i<=n;++i)
    {
        int a,b;
        a=read();
        for(int j=1;j<=a;++j)
        {
            b=read();
            b+=5000;
            addedge(i,b,1);
            addedge(b,i,0);
        }
    }
    for(int i=1;i<=n;++i)
    {
        addedge(S,i,1);
        addedge(i,S,0);
    }
    for(int i=1;i<=n;++i)
    {
        int j=i+5000;
        addedge(j,T,1);
        addedge(T,j,0);
    }
    printf("%d",xiongyali());
    return 0;
}