算法作业11——最优前缀编码

1. 问题

给定字符集C={x₁,x₂,...,x_n}和每个字符的频率f(x_i)，求关于C的一个最优前缀码。

2. 解析

①二元前缀码 ：任何字符的代码不能作为其他字符代码的前缀

②利用二元前缀码译码 ：从第一个字符开始一次读入每个字符（0 或 1），如果发现读到的子串与某个码字相等，就将这个子串译作对应的码字；然后从下一个字符开始继续这个过程，直到读完输入的字符串为止。

③二元前缀编码存储 ：二叉树结构，每个字符作为树叶，对应这个字符的前缀码看作根到这片树叶的一条路径，每个结点通向左二子的边记作 0，通向右儿子的边记作 1.

④构造最优前缀码的贪心算法就是哈夫曼算法（Huffman）:

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w₁，w₂，…，w_n，哈夫曼树的构造规则为：

　　1. 将w₁，w₂，…，w_n看成是有n 棵树的森林（每棵树仅有一个结点）；

　　2. 在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

　　3. 从森林中删除选取的两棵树，并将新树加入森林；

　　4. 重复（02）、（03）步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

 

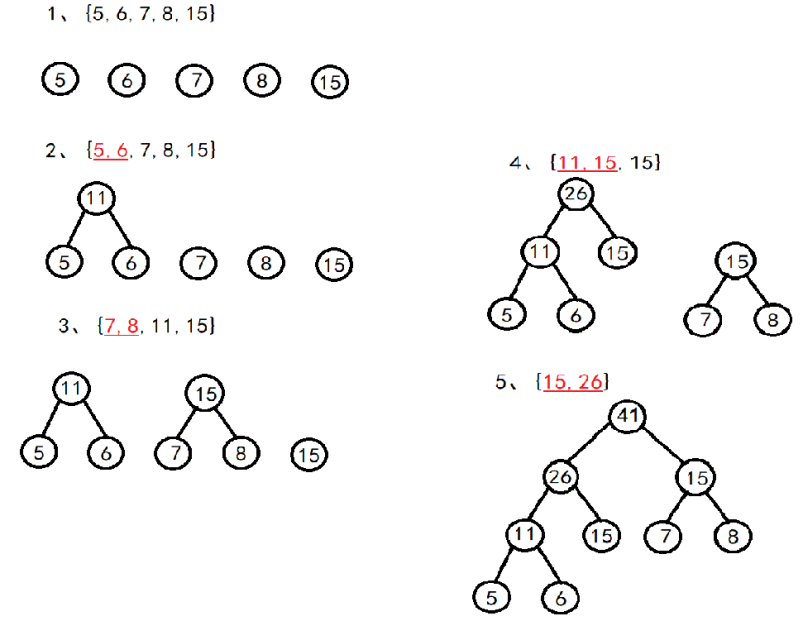
实例：

{5，6，7，8，15}

->{7,8,11,15} ->{11,15,15}

->{15,26} ->{41}

3. 设计

1. 建树（父节点、左孩子、右孩子、权值）
2. 初始化（父节点=-1、左孩子=-1、右孩子=-1、权值=0）
3. 按照权值从小到大排序，记录最小和次小根节点的序号和权值，建新树。最小节点是左孩子，次小节点是右孩子，最小和次小根节点的权值和作为新树根节点的权值加到权值序列中。
4. 重复3的步骤，直到只剩一棵单独的树。

4. 分析

for循环 O(n)，插入操作 O(logn)，

算法时间复杂度是 O(nlogn)

5. 源码

https://github.com/2579081436/algorithm.github.io