机器学习算法可以分为两大类:监督学习与非监督学习。数据集构成:‘监督学习:特征值+目标值;非监督学习:特征值’。
监督学习:
分类:K-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归、神经网络
回归:线性回归、岭回归
标注:隐马尔可夫模型
注:分类:目标值离散型数据;回归:目标值连续型数据。
无监督学习:
聚类:k-means

数据集API介绍:
sklearn.datasets 加载获取流行数据集 datasets.load_*() 获取小规模数据集,数据包含在datasets里 datasets.fetch_*(data_home = None) 获取大规模的数据集,第一次使用需要从网络上下载,时间较长,函数的第一 个参数是data_home,表示数据集的下载目录,默认是~/scikit_lean_data/
load与fetch返回的数据类型datasets.base.Bunch(字典格式)
data: 特征数据数组,是[n_samples*n_features]的二维numpy.narray数组。
target:标签数组,是n_samples的一维numpy.ndarray数组。
DESCR:数据描述。
feature_names:特征名。新闻数据,手写数字、回归数据集没有
target_names:标签名
数据集划分API:
sklearn.model_selection.train_test_split x:数据集的特征值 y:数据集的标签值 test_size:测试集的大小,一般为float random_state:随机数种子,不同的种子会造成不同的随机采样结果,相同 的随机种子采样结果相同。 return:训练集特征值,测试集特征值,训练标签,测试标签
小提示:Sklean数据集的划分比例较合理的划分:训练集,测试集。划分比列(80%-20,75%-25%,70%-30%)

from sklearn.datasets import load_iris, fetch_20newsgroups, load_boston from sklearn.model_selection import train_test_split def max_data(): # 新闻大数据——分类 news = fetch_20newsgroups(subset="all") print(news.data) print(news.target) def house_price(): # 波士顿房价——回归数据 lb = load_boston() print("获取特征值") print(lb.data) print("目标值") print(lb.target) print(lb.DESCR) pass ef mim_data(): # 鸢尾花数据(小数据集) 4个特征--分类 li = load_iris() print("获取特征值") print(li.data) print("目标值") print(li.target) print(li.DESCR) # 返回值 训练集train:x_train,y_train 测试集test:x_test,y_test x_train, x_test, y_train, y_test = train_test_split(li.data, li.target, test_size=0.25) print("训练集的特征值和目标值:", x_train, y_train) print("测试集的特征值和目标值:", x_test, y_test) return None
估计器
在sklearn中,估计器(estimator)是一个重要的角色,分类器和回归器都属于estimator,是一类实现了算法的API。
- fit方法用于从训练集中学习模型参数
- transform用学习到的参数转换数据
1、用于分类的估计器:
-
sklearn.neighbors k-近邻算法
-
sklearn.naive_bayes 贝叶斯
-
sklearn.linear_model.LogisticRegression 逻辑回归
- sklean.tree 决策树和随机森林
2、用于回归的估计器:
-
sklearn.linear_model.LinearRegression 线性回归
-
sklearn.linear_model.Ridge 岭回归
分类算法
K-近邻算法
定义:如果一个样本在特征控件中的k个最相似的样本中的大多数属于某一个类别,则该样本也属于这个类别。
注:样本距离使用欧式距离时,数据需要进行标准化处理。
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, algorithm="auto") n_neighbors: 查询默认使用的邻居数,默认为5 algorithm:{'auto','ball_tree','kd_tree','brute'},可选用于计算最近邻 居的算法:'ball_tree'将会使用BallTree,'kd_tree'将使用 KDTree。'auto'将尝试根据传递给fit方法的值来决定最合适的 算法。(不同实现方式影响效率)

def kNN(): from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import StandardScaler from sklearn.model_selection import GridSearchCV """ 预测入住位置,数据无法下载,貌似要FQ :return None """ # 读取数据 import pandas as pd #处理数据--缩小数据,删选距离为x公里内的位置, data = pd.read_csv("https://www.kaggle.com/c/facebook-v-predicting-check-ins/data") data.query('x>1.0&x<1.25&y>2.5&y<2.75') time_value = pd.to_datetime(data['time'], unit='s') # 转换时间戳 time_value = pd.DatetimeIndex(time_value) #把日期转换为字典格式 # 增加特征,增加一个day特征 data['day'] = time_value.day data['hour'] = time_value.hour data['weekday'] = time_value.weekday data.drop(["time"], axis=1) # axis=1 按列删除 # 把签到数量少于n=3的目标位置删除 place_count = data.groupby("place_id").count() tf = place_count[place_count.row_id>3].reset_index() # reset_index()索引变为一列 data = data[data['place_id'].isin(tf.place_id)] # 取出数据中的特征值和目标值 y = data["place_id"] x = data.drop(["place_id"], axis=1) # 将数据分割为训练集和测试集 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 特征工程(标准化) std = StandardScaler() x_train = std.fit_transform(x_train) x_test = std.transform(x_test) # 进行算法流程,超参数5 KNN = KNeighborsClassifier(n_neighbors=5, algorithm="auto") # fit, predict, score # KNN.fit(x_train, y_train) # y_predict = KNN.predict(x_test) #得到预测结果 # print('预测的目标签到位置为: ', y_predict) # print('预测的准确率: ', KNN.score(x_test, y_test)) # 进行网格搜素 param = {'n_neighbors': [3, 5, 10]} #构建参数值进行搜索 gc = GridSearchCV(KNN, param_grid=param, cv=2) gc.fit(x_train, y_train) #预测准确率 print('在测试集上的准确率: ', gc.score(x_test, y_test)) print("在交叉验证当中最好的结果:", gc.best_score_) print("选择的最好模型: ", gc.best_estimator_ ) print('每个超参数每次交叉验证的结果: ', gc.cv_results_) return None
K-近邻算法优缺点:
优点:简单,易于了解,易于实现,无需估计参数,无需训练
缺点:懒惰算法,对测试样本分类时的计算量大,内存开销大;必须选择K值,K值选择不当则分类精度不能保证。
使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试。
朴素贝叶斯算法



eg:
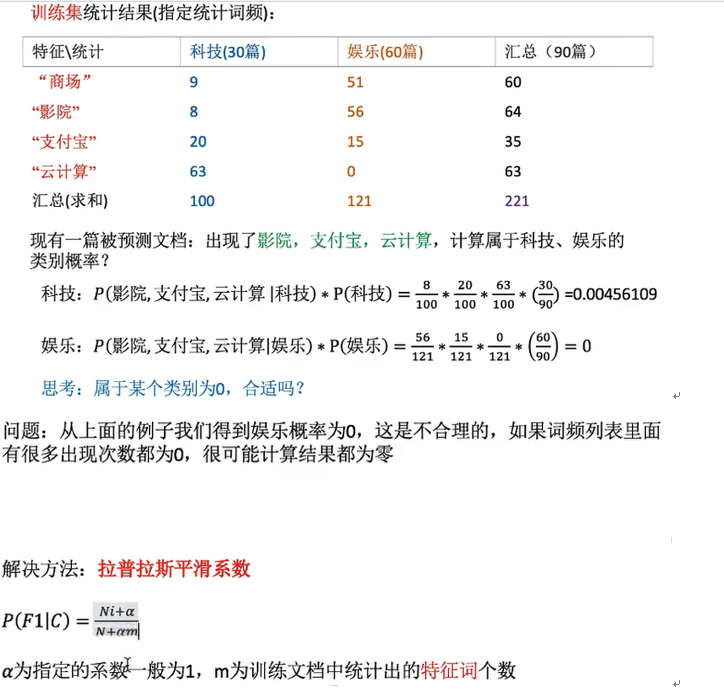
sklearn.naive_bayes.MultinomialNB(alpha=1.0)
alpha:拉普拉斯平滑系数

def neviebayes(): """ 朴素贝叶斯进行文本分类 :return: None """ from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.naive_bayes import MultinomialNB from sklearn.metrics import classification_report news = fetch_20newsgroups(subset='all') # 数据分割 x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.20) # 对数据进行抽取 tf = TfidfVectorizer() # 以训练集当中的词的列表进行每篇文章重要性统计 x_train = tf.fit_transform(x_train) print(tf.get_feature_names()) x_test = tf.transform(x_test) #进行朴素贝叶斯算法的预测,一般默认为1.0 mlt = MultinomialNB(alpha=1.0) print(x_train.toarray()) mlt.fit(x_train, y_train) y_predict = mlt.predict(x_test) print("预测的文章类别为: ", y_predict) print("准确率为: ", mlt.score(x_test, y_test)) print("每个类别的准确率和召回率: ", classification_report(y_test, y_predict, target_names=news.target_names)) return None
拉普拉斯分类算法优缺点:
优点:
- 朴素贝叶斯模型发源于古典数据理论,有稳定的分类效率。
- 对缺失数据不敏感,算法也比较简单,常用语文本分类。
- 分类精度高,速度快。
缺点:由于使用了样本属性独立性的假设,所以如果样本属性有关联时其效果不好。


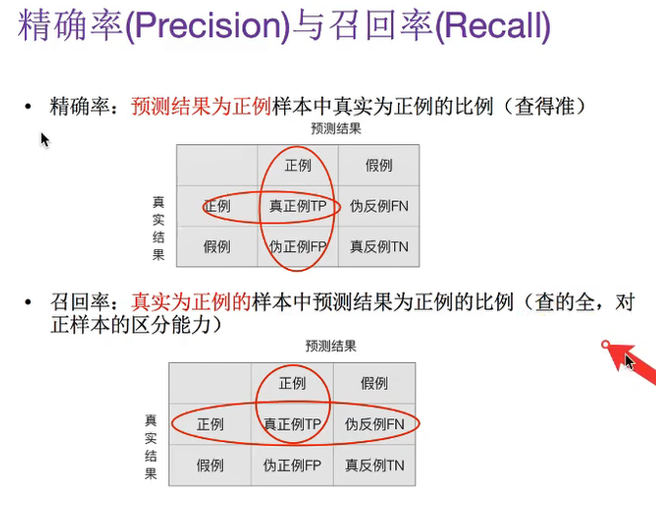
分类模型评估API

模型的选择与调优:交叉验证、网格搜索。
交叉验证:
目的:为了让被评估的模型更加准确可信。

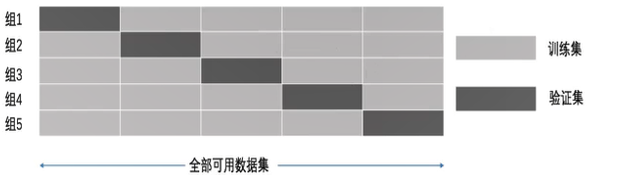
超参数搜索--网格搜索
超参数是在建立模型时用于控制算法行为的参数。这些参数不能从常规训练过程中获得。在对模型进行训练之前,需要对它们手动进行赋值。但手动过程繁杂,网格搜索是一种基本的超参数调优技术。它类似于手动调优,为网格中指定的所有给定超参数值的每个排列构建模型,评估并选择最佳模型。(是个自动的过程)

决策树与随机森林
香农公式:

信息增益:当得知一个特征条件后,减少的信息熵的大小。信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。信息增益是决策树划分的依据之一。


eg:
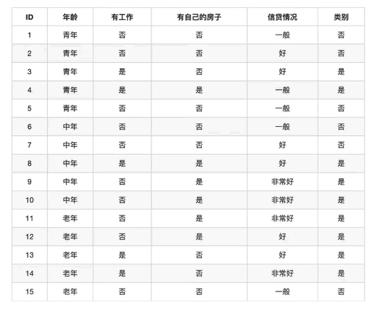

决策树使用的常见准则:
- ID3:信息增益最大准则
- C4.5:信息增益比最大准则
- CART:回归树:平方误差最小;分类树:基尼系数最小的准则
sklearn.tree.DecisionTreeClassifier(criterion='gini', max_depth=None, random_state=None) #决策树分类器 criterion:默认是'gini'系数,也可以选择信息增益的熵'entropy' max_depth:树的深度 random_state:随机数种子 decision_path:返回决策树的路径

def decision(): """ 决策树对泰坦尼克号进行预测生死 :return: None """ import pandas as pd from sklearn.metrics import classification_report from sklearn.feature_extraction import DictVectorizer from sklearn.tree import DecisionTreeClassifier, export_graphviz from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import GridSearchCV # 获取数据 titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt") # 处理数据,找出特征值和目标值 x = titan[['pclass', 'age', 'sex']] y = titan[['survived']] # 缺失值处理 x["age"].fillna(x['age'].mean(), inplace=True) # 分割数据集到训练集和测试集 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 进行处理 (特征工程 特征-》类别-》one_hot编码) dict = DictVectorizer(sparse=False) x_train = dict.fit_transform(x_train.to_dict(orient='records')) # 转换为字典 print(dict.get_feature_names()) x_test = dict.transform(x_test.to_dict(orient='records')) # # 用决策树进行预测 树的深度设置max_depth=5 # decTree = DecisionTreeClassifier(criterion='gini',max_depth=None, random_state=None) # decTree.fit(x_train, y_train) # print('预测的准确率: ', decTree.score()) # # # 导出树的结构, feature_names = dict.get_feature_names() # export_graphviz(decTree, out_file='./tree.dot', feature_names=['age', 'pclass=lst', 'pclass=2nd', 'pclass=3rd', 'sex=female', 'sex=male']) # 随机森林进行预测 rf = RandomForestClassifier() param = {"n_estimators":[120,200,200,500,800,1200], 'max_depth': [5,8,15,25,30]} # 网格搜素与交叉验证 gc= GridSearchCV(rf, param_grid=param,cv=2) gc.fit(x_train,y_train) print("准确率: ", gc.score(x_test, y_test)) print("查看选择的参数: ", gc.best_params_)
运行:dot -Tpng ./tree.dot -o image.png 将生成保存的决策树转为png格式
决策树的优缺点以及改进:
- 优点:简单的理解和解释,树木可视化;不需要对数据进行过多处理,其他技术通常需要对数据进行归一化
- 缺点:决策树学习者可以创建不能很好地推广数据的过于复杂的树。(过拟合)
- 改进:剪枝cart算法;随机森林
决策树调优——随机森林
集成学习:通过建立几个模型组合来解决单一预测问题,它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成单预测,因此优于任何一个单分类作出的预测。
随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。



随机森林的优点:
- 在当前所有算法中,具有极好的准确率
- 能够有效地运行在大数据集上
- 能够处理具有高维特征的输入样本,而且不需要降维
- 能够评价各个特征在分类问题上的重要性
回归算法
线性回归
定义:通过一个或者多个自变量与因变量之间进行建模回归分析。
一元线性回归:涉及到的变量只有一个。多元线性分析:涉及到的变量两个或者两个以上。

减少误差的两种方式:
(1)正规方程
(2)梯度下降

欠拟合原因以及解决方法:
- 原因:学习到的数据的特征过少
- 解决方法:增加数据的特征数量
过拟合原因以及解决方法:
- 原因:原始特征过多,存在一些嘈杂特征,模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决方法:进行特征选择,消除关联性大的特征;交叉验证(让所有数据都有过训练);正则化
岭回归
岭回归:回归得到的回归系数更符合实际,更可靠。另外,能让估计参数的波动范围变小,变得更稳定。在存在病态数据偏多的研究中有较大的实用价值。
逻辑回归解决分类问题(只能解决二分类)



from sklearn.datasets import load_boston from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, LogisticRegression from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.metrics import mean_squared_error, classification_report import joblib import pandas as pd import numpy as np def mylinear(): """ 线性回归预测房子价格 :return: None """ # 获取数据 lb = load_boston() # 分割数据集 x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25) print(y_train, y_test) #进行标准化处理 # 特征值 目标值都要进行标准化处理,实例化两个API # 特征值 std_x = StandardScaler() x_train = std_x.fit_transform(x_train) x_test = std_x.transform(x_test) #目标值标准化 std_y = StandardScaler() y_train = std_y.fit_transform(y_train) y_test = std_y.transform(y_test) # estimator预测 # 正规方程求解方式预测 lr = LinearRegression() lr.fit(x_train, y_train) print(lr.coef_) # 预测测试集的房子价格 y_predict = lr.predict(x_test) y_predict = std_y.inverse_transform(y_predict) print("正规方程的均方误差: ", mean_squared_error(std_y.inverse_transform(x_test), y_predict)) # # 梯度下降进行房价预测 # sgd = SGDRegressor() # sgd.fit(x_train, y_train) # print(sgd.coef_) # # 预测测试集的房子价格 # y_predict = sgd.predict(x_test) # y_predict = std_y.inverse_transform(y_predict) # print(y_predict) # print("梯度下降的均方误差: ", mean_squared_error(std_y.inverse_transform(x_test), y_predict)) # 岭回归进行房价预测 rd = Ridge(alpha=1.0) rd.fit(x_train, y_train) print(rd.coef_) # #保存训练好的模型 # joblib.dump(rd, './tmp/test.pkl') # # 导入训练好的模型 # model = joblib.load('./tmp/test.pkl') # y_predict = std_y.inverse_transform(model.predict(x_test)) # 预测测试集的房子价格 y_predict = rd.predict(x_test) y_predict = std_y.inverse_transform(y_predict) print("岭回归的均方误差: ", mean_squared_error(std_y.inverse_transform(x_test), y_predict)) return None def logistic(): """ 逻辑回归做二分类 :return: """ # 构建列名 column = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape', 'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin ', 'Normal Nucleoli', ' Mitoses', 'Class'] # 读取数据 data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data", names=column) print(data) # 缺失值处理 data = data.replace('?', np.nan) data = data.dropna() # 分割数据 x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]],data[column[10]], test_size=0.25) # 进行标准化处理 std = StandardScaler() x_train = std.fit_transform(x_train) x_test = std.transform(x_test) # 逻辑回归预测 lg = LogisticRegression(C=1.0) lg.fit(x_train, y_train) print(lg.coef_) y_predict = lg.predict(x_test) print("准确率: ", lg.score(x_test, y_test)) print('召回率: ', classification_report(y_test, y_predict, labels=[2, 4], target_names=['良性', '恶性'])) return None if __name__ == "__main__": logistic()
无监督学习——K-means

sklearn.cluster.KMeans

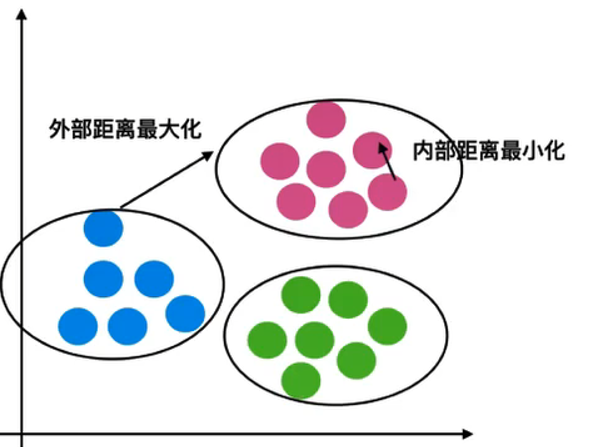
轮廓系数[-1,1],趋势近于1代表内聚度和分离度都相对较优。( 外部距离最大,内部距离最小)

