Description
如果一个字符串S是由一个字符串T重复K次形成的,则称T是S的循环节。使K最大的字符串T称为S的最小循环节,此时的K称为最大循环次数。
现给一个给定长度为N的字符串S,对S的每一个前缀S[1~i],如果它的最大循环次数大于1,则输出该前缀的最小循环节长度和最大循环次数。
Input
输入包含多组数据,每组数据第一行为正整数n(2≤n≤1000000),第二行为一个字符串S。
输入结束标志为n=0
Output
输出: 对于每组数据,按照从小到大的顺序输出每个i和对应的K,一对整数占一行。
(KMP)的好题啊。
为什么会是(KMP)?
考虑这个串是给定的,必然循环的一个串,我们还需要找到的是所有前缀串的最大循环次数。
由于是一个循环串,那么其前缀和后缀必然相等.所以我们考虑到了(KMP)算法.
如何解?
想到了是(KMP)算法,但是我们不可能直接通过判断当前(i % next[i]==0)来解决此题(样例都出不来好吧.)
考虑一下我们(next)数组的定义:
最长公共前后缀的长度.
注意这个(next)数组长度不可能为原串长度.
(这就能体现出你(KMP)学的怎么样了)
这时考虑(i-next[i])代表着什么。
(i-next[i])代表循环节长度.
为什么?
我们对于一个循环串输出一下其(next)数组.
这样
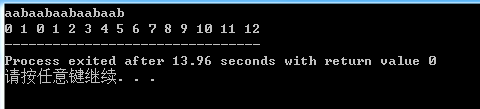
因为我们用(i-next[i])即可求出循环节的长度.
又因为(next)数组记录的是最长的.因此这个循环节一定是最短的.
代码
#include<cstdio>
#include<cstring>
#define R
using namespace std;
char s[1000008];
int n,nex[1000008],len,cas;
int main()
{
while(~scanf("%d",&n))
{
if(n==0)break;
scanf("%s",s+1);
int k=0;nex[1]=0;
printf("Test case #%d
",++cas);
for(R int i=2;i<=n;i++)
{
while(k and s[k+1]!=s[i])k=nex[k];
if(s[k+1]==s[i])k++;
nex[i]=k;
}
for(R int i=1;i<=n;i++)
printf("%d ",nex[i]);
puts("");
for(R int i=2;i<=n;i++)
{
if(nex[i]==i)continue;
if(i%(i-nex[i])==0 and i/(i-nex[i])>1)
printf("%d %d
",i,i/(i-nex[i]));
}
memset(nex,0,sizeof nex);
puts("");//注意这里还有一个换行
}
}