Description
小明要去一个国家旅游。这个国家有(N)个城市,编号为(1)至(N),并且有(M)条道路连接着,小明准备从其中一个城市出发,并只往东走到城市(i)停止。
所以他就需要选择最先到达的城市,并制定一条路线以城市(i)为终点,使得线路上除了第一个城市,每个城市都在路线前一个城市东面,并且满足这个前提下还希望游览的城市尽量多。
现在,你只知道每一条道路所连接的两个城市的相对位置关系,但并不知道所有城市具体的位置。现在对于所有的(i),都需要你为小明制定一条路线,并求出以城市(i)为终点最多能够游览多少个城市。
Input
第(1)行为两个正整数(N, M)。
接下来(M)行,每行两个正整数(x, y),表示了有一条连接城市(x)与城市(y)的道路,保证了城市(x)在城市(y)西面。
Output
(N)行,第(i)行包含一个正整数,表示以第(i)个城市为终点最多能游览多少个城市。
刚开始看不出来是个啥题,隐隐约约觉得是(Topsort)
敲了一通,交上去,Wa声一片
然后把一个位置改成了取(max)就A了。。。就那么A了。。。
为什么是(Topsort)?
首先画图观察样例.是这样的
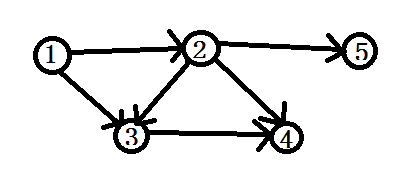
我们发现,只有当一个点的入度全部被删去的时候,就能得到以其为重点最多能游览的城市.
因此想到了(Topsort)
至于为什么我第一遍没有(A)掉
其实是第一遍拓扑排序写错了
然后需要注意的是要对到达的点取(max).
这里(to[i])代表以(i)为终点时,最多经过多少个城市.
[to[v]=max(to[v],to[u]+1)
]
代码
#include<cstdio>
#include<cctype>
#include<iostream>
#define N 100008
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,m,head[N],tot,ins[N],stk[N],to[N],top;
struct cod{int u,v;}edge[N<<1];
inline void add(int x,int y)
{
edge[++tot].u=head[x];
edge[tot].v=y;
head[x]=tot;
}
inline void topsort()
{
while(top)
{
int u=stk[top--];
for(R int i=head[u];i;i=edge[i].u)
{
ins[edge[i].v]--;
to[edge[i].v]=max(to[u]+1,to[edge[i].v]);
if(!ins[edge[i].v])
stk[++top]=edge[i].v;
}
}
for(R int i=1;i<=n;i++)printf("%d
",to[i]);
}
int main()
{
in(n),in(m);
for(R int i=1,x,y;i<=m;i++)
{
in(x),in(y);
ins[y]++;
add(x,y);
}
for(R int i=1;i<=n;i++)
{
to[i]=1;
if(ins[i]==0)stk[++top]=i;
}
topsort();
}