模拟【p2239】 螺旋矩阵

顾z

你没有发现两个字里的blog都不一样嘛 qwq

题目描述--->p2239 螺旋矩阵

看到题,很明显,如果直接模拟的话,复杂度为(O(n^2))过不去.(这个复杂度应该不正确,我不会分析的啊 qwq.

因此我们需要一个比较厉害的方法解决这个题,

前置知识

我们手写一些矩阵,发现我们填的数是会分层的 ！.

(同种颜色为一层.)

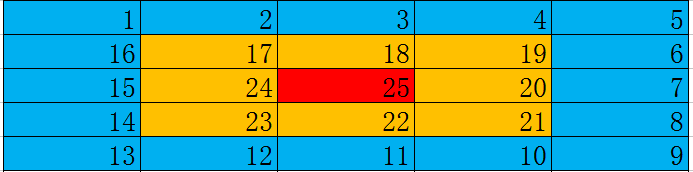
分层这个东西的话,我也不能具体解释,你可以认为是一圈一圈地填数.

xjb分析

打表!找规律

我们可以手写一个程序,(也可以手写,手写的话会更简单一些.)

模拟一下这个过程.

例如这个程序(话说,打个表我想了半小时? qwq 一定是我太垃圾了

下面的变量(ceng)的话,是因为构造出来的矩阵会分层。

void get(int n)
{
    int cnt=0,x=1,y=1;
    for(R int ceng=1;ceng<=(n+1)/2;ceng++)
    {
    	while(y<=n-ceng+1)
    		res[x][y++]=++cnt;x++;y--;
    	while(x<=n-ceng+1)
    		res[x++][y]=++cnt;x--;y--;
    	while(y>=ceng)
    		res[x][y--]=++cnt;y++;x--;
    	while(x>ceng)
    		res[x--][y]=++cnt;x++;y++;
    }
    print();
}

打出来5*5的表是这样的 qwq

开始搬砖找规律.

1. 第(1)行第(j)列对应的数就是j
2. 第n列第(i)行对应的为(n+i-1)
3. 第n行第(j)列对应的数为$3 imes n-j-1 $
4. 再度填回第(1)列,第(i)行我们发现得到的对应数为 (4 imes n-i-2)

上面四点是最容易发现的规律,也是我们继续求解的关键.

注意: 如果上面四条规律并没有找到的话,希望大家能自己手推找一下规律.

(PS： 本人开始用6*6的表格找规律,结果第四条规律找错 qwq)

如何填充里层的数?

我们发现17这个位置与16是有关的.而16,又是(4 imes5-4)

(多打几个表容易发现,第(2)行第(1)列这个位置的数为(4 imes n-4))

直接推导这个(4 imes n-4)的话是这样的

看图↓

我们黄色部分可以填充(n)个数,绿色部分由于黄色部分占领了一个格子,所以填充个数为(n-1)个,同理蓝色部分也只能填充(n-1)个数,红色部分由于上面有黄色部分,下面有蓝色部分,只能填充(n-2)个数.

总的来说,每一层共可以填充(4 imes n-4)个数

然后考虑搞事。

我们将更里层的数减去(4 imes n-4),得到新的里层数据如下.

这时候你可能会大吼.

“woc!又让我填一遍?”

恍然大悟

我们发现,这样的话,我们又填一次这个矩阵,不过这个矩阵的大小从(n)变成了(n-2)

(消去了,最左和最右两边.)

而假设我们之前要查找的数的位置为((4,4))就变成了((3,3))

如果是((3,4))就变成了((2,3)),

所以说,当我们求内层的时候,所求原数的位置(x,y)就将变成(x-1,y-1).

而对于那些直接满足上面我们发现的规律的数的话,我们可以直接输出.

所以不必考虑这些数的输出怎么办.

最终我们一定会拆到最里层.

以此类推

我们一直拆下去,每次加上的答案就是(4 imes n-4)。

注意:这个n是在变化的.

因此我们可以码出代码

#include<bits/stdc++.h>
#define R register 
using namespace std;
inline void in(int &x) 
{
    int f=1;x=0;char s=getchar();
    while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
    while(isdigit(s)){x=x*10+s-'0';s=getchar();}
    x*=f;
}
int n,x,y,ans;
int main()
{
    in(n),in(x),in(y);
    //如果刚开始的话x,y就满足四条规律.
    //我们会在第一次输出答案,此时ans为0,无影响.
    here:;
    if(x==1)printf("%d",y+ans);
    else if(y==n)printf("%d",n+x-1+ans);
    else if(x==n)printf("%d",3*n-y-1+ans);
    else if(y==1)printf("%d",4*n-x-2+ans);
    else
    {
        ans+=4*n-4;
        x--,y--,n-=2;
        goto here;
        //这句话达到了递归的效果。
        //我们的程序运行到这一步会到达上面的here,即再度执行这些if语句.
    }
}