转载自 从B树、B+树、B*树谈到R 树
1.用阶定义的B树
B 树又叫平衡多路查找树。一棵m阶的非空B 树的特性如下:
(注:切勿简单的认为一棵m阶的B树是m叉树,虽然存在四叉树,八叉树,KD树,及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树,但与B树完全不等同)
-
树中每个结点最多含有m个子树(m ≥ 2);
-
除根结点和叶子结点外,其它每个结点至少有┌m / 2┐个子树;
-
若根结点不是叶子结点,则至少有2个子树。若树非空,则根至少有1个关键字,故若根不是叶子,则它至少有2棵子树;
-
所有叶子结点都出现在同一层,叶子节点没有孩子和指向孩子的指针,叶子节点不包含关键字信息(可以看做是外部接点或查询失败的接点,实际上这些结点不存在,指向这些结点的指针都为null)。这里的叶子结点情况可以看下图

如图,最底层的叶子结点没有存储任何信息
a) Ki (i=1...n)为关键字,且关键字按顺序升序排序K(i-1)< Ki。
b) Pi为指向子树的根结点,且指针P(i-1)指向子树中所有关键字小于Ki,大于K(i-1)的一组结点。
c) 即每个每个非根的内部结点至少应有┌m / 2┐-1个关键字,至多有m-1个关键字。
d) 因为每个内部结点的度数正好是关键字总数加1,故每个非根的内部结点至少有┌m / 2┐棵子树,至多有m棵子树。

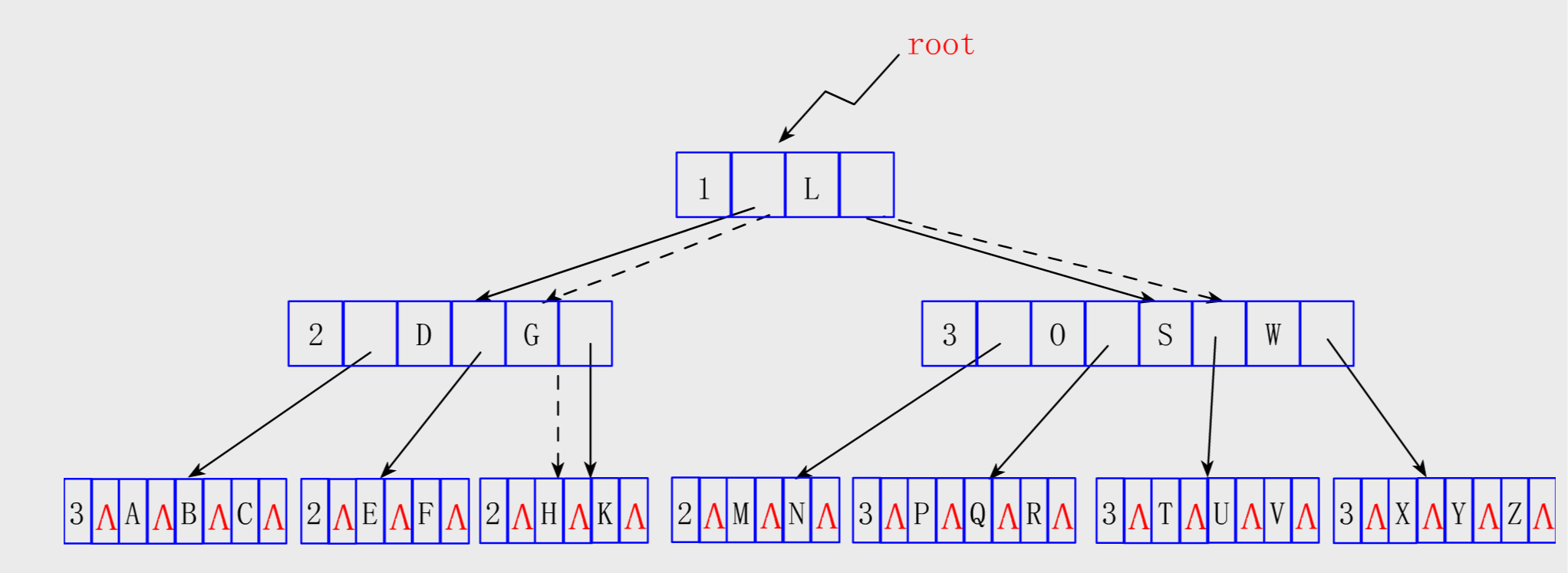
说明:
按照定义,在5阶B树里,根结点中的关键字数目可以是1~4(整棵树只有1个关键字),子树数可以是2~5;其它的结点中关键字数目可以是2~4【 ┌m / 2┐-1 ≤ n ≤ m-1】,若该结点不是叶子,则它可以有3~5棵子树【┌m / 2┐ ≤ n ≤ m】。注意子树和关键字是不一样的
网站:http://student.zjzk.cn/course_ware/data_structure/web/chazhao/chazhao9.3.2.2.htm
2.B树的高度
若B树某一非叶子节点包含N个关键字,则此非叶子节点含有N+1个孩子结点,而所有的叶子结点都在第K层,我们可以得出:- 因为根至少有两个孩子,因此第2层至少有两个结点。
- 除根和叶子外,其它结点至少有┌m/2┐个孩子,
- 因此在第3层至少有2*┌m/2┐个结点,
- 在第4层至少有2*(┌m/2┐^2)个结点,
- 以此类推
- 在第K层至少有2*(┌m/2┐^(k-2) )个结点,于是有: N+1 ≥ 2*┌m/2┐^(k-2);
- 考虑第K层的结点个数为N+1,因为2*(┌m/2┐^(k-2))≤N+1,也就是L层的最少结点数刚好达到N+1个,即: k≤ log┌m/2┐((N+1)/2 )+2;
- 当B树包含N个关键字时,B树的最大高度为k-1(因为计算B树高度时,叶结点所在层不计算在内),即:k - 1 = log┌m/2┐((N+1)/2 )+1。
B+-tree:是应文件系统所需而产生的一种B-tree的变形树。
一棵m阶的B+树和m阶的B树的异同点在于:
1.有n棵子树的结点中含有n-1 个关键字; (此处颇有争议,B+树到底是与B 树n棵子树有n-1个关键字 保持一致,还是不一致:B+树n棵子树的结点中含有n个关键字,待后续查证。暂先提供两个参考链接:①wikipedia http://en.wikipedia.org/wiki/B%2B_tree#Overview;②http://hedengcheng.com/?p=525。)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)
简单点说:
1).非叶子结点的子树指针与关键字个数相同;
2).非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);

3).为所有叶子结点增加一个链指针;

4).所有关键字都在叶子结点出现
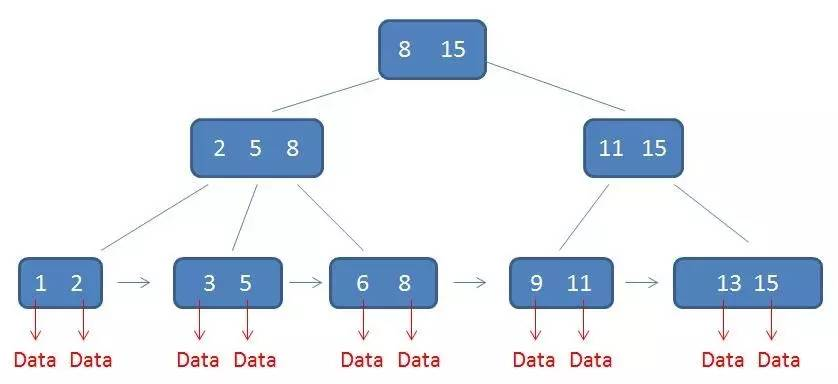
挺有用的网址:http://www.sohu.com/a/156886901_479559
B+的特性:
1).所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2).不可能在非叶子结点命中;
3).非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4).更适合文件索引系统;
B+树的优势:
1.单一节点存储更多的元素,使得查询的IO次数更少。
2.所有查询都要查找到叶子节点,查询性能稳定。
3.所有叶子节点形成有序链表,便于范围查询
磁盘中B+树索引:
局部性原理与磁盘预读,预读的长度一般为页(page)的整倍数,(在许多操作系统中,页得大小通常为4k)
数据库系统巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入,(由于节点中有两个数组,所以地址连续)。
MYSQL-B+TREE索引原理
B+树实现
【算法】B+树的研读及实现(2)---java版核心代码
B+树实现磁盘存储
可视化
https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html