一、选择排序
算法原理
- 比较未排序区域的元素,每次选出最大或最小的元素放到排序区域。
- 一趟比较完成之后,再从剩下未排序的元素开始比较。
- 反复执行以上步骤,只到排序完成。
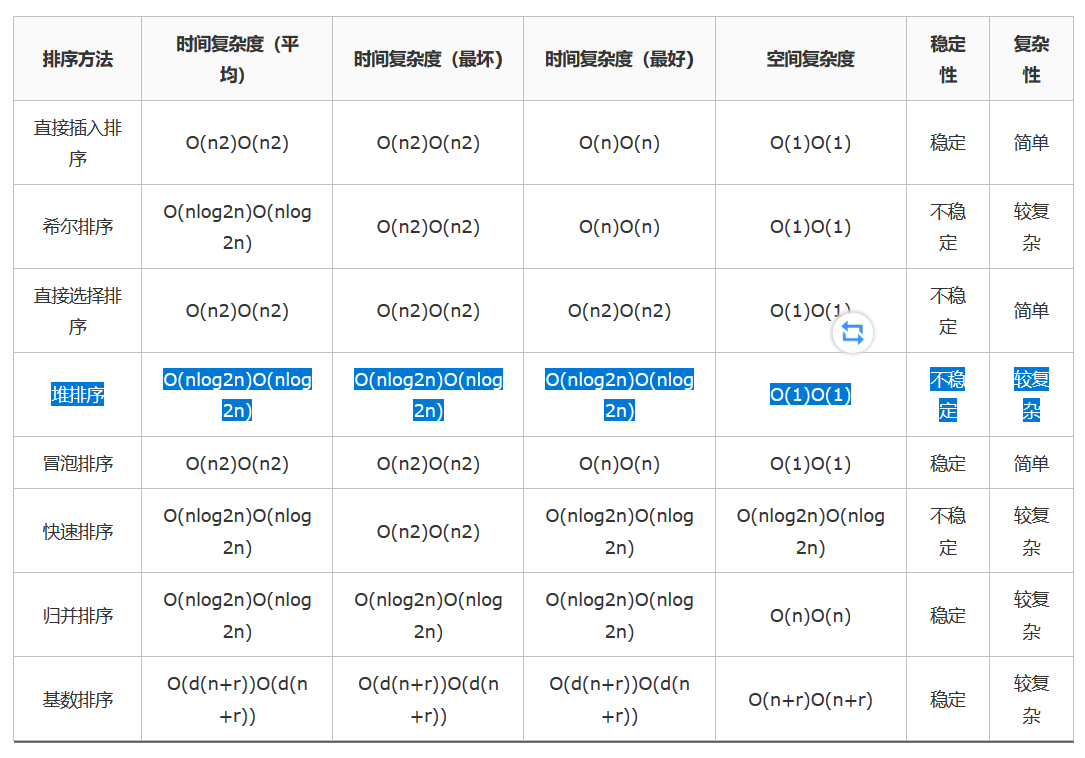
时间复杂度

图示
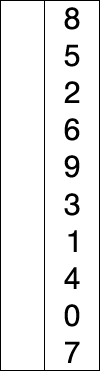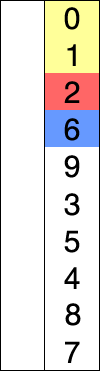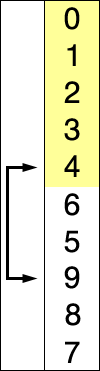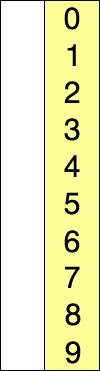
代码:
void quick_pow(int n,int a[]) { for(int i=0;i<n;i++) { int pos=i; for(int j=i+1;j<n;j++) { if(a[j]<a[pos]) pos=j; } int temp=a[i]; a[i]=a[pos]; a[pos]=temp; } }
二、冒泡排序
算法原理
-
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
-
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
时间复杂度

图示
代码
void quick_pow(int n,int a[]) { for(int i=0;i<n-1;i++)//n个元素进行n-1次排序 { for(int j=0;j<n-i-1;j++)//每趟排序比较的次数 { if(a[j]>a[j+1]) { int temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; } } } }
三、插入排序
算法原理
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序
时间复杂度

图示
代码
void quick_pow(int n,int a[]) { for(int i=1;i<n;i++)//从第二个元素开始插入,[0,i-1]都是有序数据 { int temp=a[i];//要插入的元素 int j; for(j=i-1;j>=0&&temp<a[j];j--) a[j+1]=a[j];//往右偏移,给插入的地方空出一个位置 a[j+1]=temp; } }
四、快速排序
算法原理
快速排序的本质就是把基准数大的都放在基准数的右边,把比基准数小的放在基准数的左边,这样就找到了基准在数组中的正确位置.
以后采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时该数组就自然有序了。
时间复杂度

时间复杂度最坏的情况出现再已经是有序的情况下(递增、递减、相等)
图示

代码
int find(int le,int ri,int a[])//找基准元素位置 { int base=a[le];//基准元素 while(le<ri) { while(le<ri&&a[ri]>=base)//从序列右端开始处理,大于基准的不变 ri--; a[le]=a[ri];//小于基准的交换到左边 while(le<ri&&a[le]<=base)//处理左端,小于基准的不变 le++; a[ri]=a[le];//大于基准的交换到右边 } //当左边的元素都小于base,右边的元素都大于base时,此时base就是基准元素,le或ri就是基准元素的位置 a[le]=base; return le; } void quick_pow(int le,int ri,int a[]) { if(le>=ri) return; int pos=find(le,ri,a); quick_pow(le,pos-1,a); quick_pow(pos+1,ri,a); }
①先从队尾开始向前扫描且当low < high时,如果a[high] > tmp,则high–,但如果a[high] < tmp,则将high的值赋值给low,即arr[low] = a[high],同时要转换数组扫描的方式,即需要从队首开始向队尾进行扫描了
②同理,当从队首开始向队尾进行扫描时,如果a[low] < tmp,则low++,但如果a[low] > tmp了,则就需要将low位置的值赋值给high位置,即arr[low] = arr[high],同时将数组扫描方式换为由队尾向队首进行扫描.
③不断重复①和②,知道low>=high时(其实是low=high),low或high的位置就是该基准数据在数组中的正确索引位置.
五、希尔排序(优化后的插入排序)
算法原理
希尔排序是记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
时间复杂度

图示
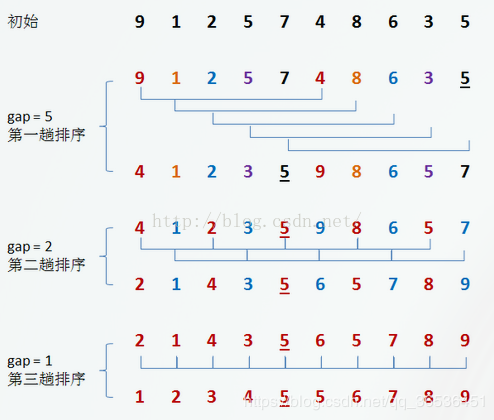
代码
void quick_pow(int n,int a[]) { for(int k=n/2;k>0;k=k/2)//k是分组距离 { for(int i=k;i<n;i++)//可以分成n-k组,轮流对每个分组进行插入排序 { int temp=a[i];// int j; for(j=i-k;j>=0&&a[j]>temp;j=j-k) a[j+k]=a[j];//前面的元素大于右边,交换位置, a[j+k]=temp; } } }
六、归并排序
算法原理
归并排序的核心思想是将两个有序的数列合并成一个大的有序的序列。通过递归,层层合并,即为归并。
时间复杂度

图示
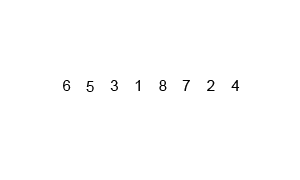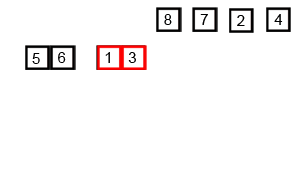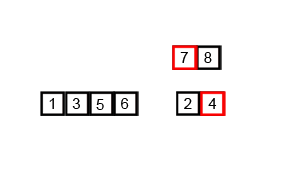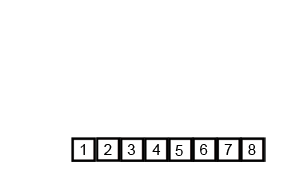
先把整体二分到一,在合并成有序整体
代码
void merge(int le,int mid,int ri,int a[],int temp[])//将数组a的左右两部分合并 { int i=le,j=mid+1; int m=mid,n=ri; int k=0; while(i<=m&&j<=n)//a数组两端更小的先加进temp数组 { if(a[i]<a[j]) temp[k++]=a[i++]; else temp[k++]=a[j++]; } //把a数组剩下的部分加入temp数组 while(i<=m) temp[k++]=a[i++]; while(j<=n) temp[k++]=a[j++]; for(int i=0;i<k;i++)//把有序的temp数组放回a数组 a[le+i]=temp[i]; } void quick_pow(int le,int ri,int a[],int temp[]) { if(le>=ri) return ; int mid=(le+ri)/2; quick_pow(le,mid,a,temp);//使左边有序 quick_pow(mid+1,ri,a,temp);//右边有序 merge(le,mid,ri,a,temp);//左右有序的部分合并 }
七、堆排序
算法原理
堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
-
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
-
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
图示
-
创建一个堆 H[0……n-1],按照大顶堆的性质从左往右创建;
-
创建完成之后,先把堆首元素(最大值)拿走,再把堆尾元素(同一层按从右往左顺序)放到堆首位置;
-
堆尾元素放到堆首之后,判断是否比左右节点元素大,交换使堆顶元素大于左右节点;
-
重复步骤 2,直到堆的尺寸为 1。

代码
#include<iostream> #include<algorithm> #include<math.h> #include<string.h> #define ll long long #define M 0x3f3f3f3f3f using namespace std; void quick_pow(int a[],int pos,int len) { int root=a[pos];//顶点 int le=pos*2+1;//因为pos使从0开始,所以是左孩子 while(le<len) { int ri=le+1; if(ri<len&&a[ri]>a[le])//使左孩子大于右孩子 le=ri; if(root<a[le])//使顶点大于左孩子 { a[pos]=a[le]; pos=le; le=pos*2+1; } else break; } a[pos]=root; } void init(int n,int a[]) { for(int i=n/2-1;i>=0;i--)//将数组a初始化为大顶堆 quick_pow(a,i,n); for(int i=n-1;i>=0;i--)//将堆顶元素和堆尾元素互换,并维护大顶堆的性质 { int temp=a[0];//堆顶元素 a[0]=a[i]; a[i]=temp; quick_pow(a,0,i); } } int main() { int n; int a[105],temp[105]; cin>>n; for(int i=0;i<n;i++) cin>>a[i]; init(n,a); for(int i=0;i<n;i++) cout<<a[i]<<' '; cout<<endl; return 0; }
排序算法稳定性的理解
假定在待排序的记录序列中, 存在多个具有相同关键字的记录, 若经过排序, 这些记录的相对次序保持不变
即:在原序列中, a=b, 且a在b之前, 而排序后, a仍在b之前, 则称为这种排序算法是稳定的, 否则称为不稳定的.
如1,44,22, 55,22,99.
原始数列中,有两个22. 按颜色区分相对次序。
那么稳定性排序完成后就该为:
1, 22, 22, 44, 55, 99
不稳定性排序完成后可能为:
1, 22,22, 44, 55, 99
稳定性排序的意义或优点:
如果单纯的对数字讨论它的稳定性是毫无意义的(只有一个键),只有对多个键(属性)的值稳定性才有意义(和结构体排序很像)
排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。
举个例子:
对销售数据进行排序,一个销售数据的属性包括销量和单价,如今需要按照销量高低排序,使用稳定性算法,
可以使得想同销量的对象依旧保持着价格高低的排序展现,只有销量不同的才会重新排序。