Catalan数
还记2016年的那道选择题被安排到了55级的数学学案上的01规范数列:
定义“规范(01)数列”({a_n})如下:({a_n})共有(2m)项,其中(m)项为(0),(m)项为(1),且对任意(k≤2m),(a_1),(a_2),…,(a_k)中0的个数不少于1的个数,若(m=4),则不同的“规范(01)数列”共有多少个()
(A、18) (B、16) (C、14) (D、12)
又记清华测试2021年一月的填空
现将大小形状相同的4个黑色球和4个红色球排成一排,从左边第一个球开始数,不管数几个球,黑球数不少于红球数的排法有___种
作为做过这题三次起步的小F,当然直接秒了这个题。(当然事后被小x谴责了...)
但当时只知道它是卡特兰数并知道它的公式是(C^n_{2n}-C^{n+1}_{2n}),但并不知道是怎么证明的,但现在小F知道了!2021.1.29
Catalan数
1 定义:由(n)个(1)和(n)个(0)组成的有(2n)个数的数,且从左到右(0)的累计数不小于(1)的累计数的方案种数
2 分析一下该问题可等价于求从(A)点到(B)点不超过红线(可接触)的最短路径数量,把向右走看成(0),把向上走看成(1),超过红线说明1向上走的多了,即为(1)的个数多于(0)的个数了。
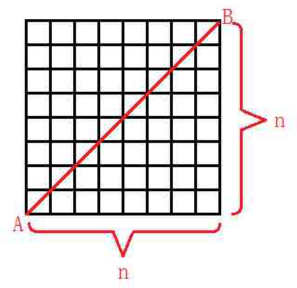
3 题目相当于求从((0,0))走到((n,n))且不跨越直线(y=x)的方案数。首先,如果不考虑不能跨越直线(y=x)的要求,相当于从(2n)步中选(n)步向右走,选(n)步向上走,则方案数为(C^n_{2n})。然后,考虑对于一种不合法的方案,一定在若干步后有一步越过了(y=x)到了(y=x+1),这个点在直线(y=x+1) (即下图中红色的线) 上。那么把第一次碰到该直线以后的部分关于该直线对称,则最终到达的点是((n−1,n+1)) (如下图) 。