「Wallace 笔记」点分治详解

Part 0 - 简介

点分治是一种树上的分治算法，是处理树上路径问题的常用算法。

比如 POJ 1741 - Tree 这道题：

给定一颗 (n（le 10^4）) 个结点的树，每条边都有长度（(le 10^3)）。求树上总长度不超过 (k) 的路径的数量。

暴力搜索的复杂度是 (O(n^2)) 的，显然无法通过，于是就需要点分治处理这种问题。

下文是以本题为例题，对点分治到底详细介绍。

Part 1 - 点分治详解

Part 1.1 - 分治方法

首先，我们选择一个根（分治中心），将无根树转化为有跟树。

那么树上的所有路径可以分为两类：

1. 不经过根结点的路径。

2. 经过根节点的路径。

第一种我们可以通过递归处理子树的方法完成，现在主要处理第二种。

Part 1.1.1 - 容斥法

假如我们在以当前分治中心的子树上 DFS，将所有连接分治中心与子树中结点的路径的长度信息 导出到一个数组中 ，然后 排序 ，就可以使用 类似于双指针的方法 计算出其中符合条件的数对的对数，即 路径的对数。

但这样的话，某一个路径对拼接而成的路径 可能经过某条边不止一次 ，我们需要防止这种不合法的情况出现，即 确保路径的两端必须来自不同的子树中 。容斥法的处理方法就是，用同样的方法去计算当前分治中心所有子树的路径对数，然后当前的对数要 减去这些子树中的对数，剩下的就是合法的路径。

容斥法的优点在于，简单方便，非常套路—— 就是计算整个的，减去所有各个子树的和 。缺点就是是，并不是所有问题都可以使用容斥法的 。

Part 1.1.2 - 顺序处理方法

另一种方法。具体地，假设当前处理到第 (k) 个子树，而第 (1sim k-1) 个子树都以及处理完了。还是先导出子树 (k) 的所有路径信息，然后 将这些路径信息与的路径前 (k-1) 个子树信息配对 。这样非常自然地避开了重边的不合法情况。

如何妥善处理前 (k-1) 个子树的信息？ 使用合适的数据结构 。一开始，还没有任何子树被处理，数据结构应是空的状态。每当处理完一个子树（已经完成配对和统计答案了），就 把这个子树的信息添加到数据结构中 。差不多按这样的套路做下去即可。

这样的方法的优点在于， 可以处理容斥法所不能处理的问题 。缺点就是，如果可以容斥，没有容斥法方便（容斥法中的计算路径对数通常可以压缩成一个函数来减少代码复杂程度）；每次分治后必须妥善清除数据结构中的信息。

Part 1.1.3 染色法

一种不常用的方法。

首先还是像容斥法一样，导出以分治中心为根的路径信息。要使路径两端一定要在不同子树中，我们其实可以 做一个标记 ，记录一下这些路径分别是穿过哪颗子树的，统计是加一个判断即可。

优点是思路简单，缺点是麻烦。

Part 1.2 - 重心分解优化

很快，你又会意识到一个新的问题：如果对分治中心的选择不恰当，整个算法还是会退化为 (O(n^2))。

当树成为近乎或就是一条链的形状时，如图：

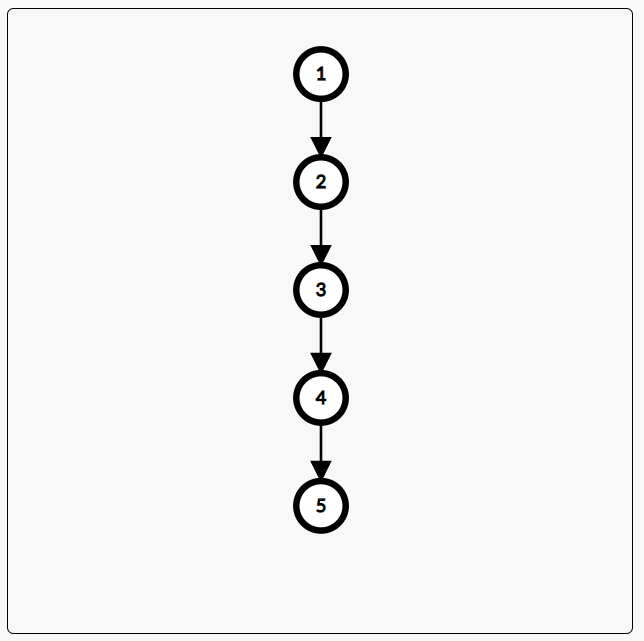
如果选取的分治中心分别为：(1,2,3,4,5) 的话，一共要做 (4+3+2+1) 的常数倍次计算，也就是退化成 (O(n^2)) 的算法了。

瓶颈在于选取分治中心后，部分子树的 深度 过大。但如果我们选取 树的重心 作为分治中心，那么这个问题就可以有效解决了。

其中的精妙之处在于重心的一个性质—— 一颗 (n) 个结点的树，以重心为根，得到的所有子树，结点数不超过 (frac{n}{2}) ，因此递归的深度一定不超过 (O(log n))。具体证明并不复杂，可以尝试自己证明。

如是，一直选取子树的重心作为分治中心的话，根据主定理，整个算法的复杂度就会控制在 (O(nlog^2 n))。（其中排序有一个 (log)，但如果用到的是一些其他复杂度（(k)）的数据结构，复杂度就是 (O(nlog n imes k))）

为避免重复进入某个点，我们用一个标记（下面代码的 centr ），记录一下这个点曾经有没有被作为分治中心标记过，下次就不用进入这样的点了。

Part 1.3 - 代码实现

Luogu P4178 Tree 代码。（POJ不能用 c++11）

容斥法实现，时间复杂度 (O(nlog^2 n))：

/*
 * Author : _Wallace_
 * Source : https://www.cnblogs.com/-Wallace-/
 * Article : 点分治详解 
 */
#include <algorithm> 
#include <cstdio>
#include <vector>

using namespace std;
const int N = 4e4 + 5;

int n, k, ans = 0;
struct edge { int to, len; };
vector<edge> G[N];

bool centr[N]; // 重心标记 
int size[N]; // 子树大小 
int root, maxp[N]; // 重心，找重心的辅助数组 

int getSize(int x, int f) { // 计算子树大小 
	size[x] = 1;
	for (auto y : G[x])
		if (y.to != f && !centr[y.to])
			size[x] += getSize(y.to, x);
	return size[x];
}
void getCentr(int x, int f, int t) { // 找重心，其中 t 表示整个连通块的大小 
	maxp[x] = 0;
	for (auto y : G[x]) {
		if (y.to == f || centr[y.to]) continue;
		getCentr(y.to, x, t);
		maxp[x] = max(maxp[x], size[y.to]);
	}
	maxp[x] = max(maxp[x], t - size[x]);
	if (maxp[x] < maxp[root]) root = x;
}

int dis[N], tot = 0;
void getDist(int x, int f, int d) { // 路径导出 
	dis[++tot] = d; // 加入信息 
	for (auto y : G[x])
		if (y.to != f && !centr[y.to])
			getDist(y.to, x, d + y.len);
}

int count(int x, int d) { // 计算对数，d 表示到分治中心的距离 
	tot = 0, getDist(x, 0, d); // 导出路径的信息 
	sort(dis + 1, dis + 1 + tot); // 排序，便于使用双指针 
	int ret = 0, l = 1, r = tot; // 双指针计算对数 
	while (l < r) (dis[l] + dis[r] <= k) ? (ret += r - l, ++l) : (--r);
	return ret;
}

void solve(int x) {
	getSize(x, 0);
	maxp[root = 0] = N;
	getCentr(x, 0, size[x]);
	int s = root; // 找重心，现在分治中心为 s 
	centr[s] = true; // 标记重心 
	
	for (auto y : G[s])
		if (!centr[y.to])
			solve(y.to); // 递归处理不经过分治中心的路径 
	
	ans += count(s, 0); // 先加上所有的对数 
	for (auto y : G[s])
		if (!centr[y.to])
			ans -= count(y.to, y.len); // 容斥一下，减去在同一个子树的对数 
	
	centr[s] = false; // 清除标记 
}

signed main() {
	scanf("%d", &n);
	for (register int u, v, l, i = 1; i < n; i++) {
		scanf("%d%d%d", &u, &v, &l);
		G[u].push_back({v, l});
		G[v].push_back({u, l});
	}
	scanf("%d", &k);
	solve(1); // 算法主体 
	printf("%d
", ans);
	return 0;
}

顺序处理方法，使用常数略小的树状数组实现。复杂度 (O(nlog nlog k))。

如果写平衡树复杂度为 (O(nlog^2 n))。

/*
 * Author : _Wallace_
 * Source : https://www.cnblogs.com/-Wallace-/
 * Article : 点分治详解 
 */
#include <algorithm>
#include <cstdio>
#include <vector>

using namespace std;
const int N = 4e4 + 5;
const int K = 2e4 + 5;

int n, k;
namespace bit {
	#define lbt(x) (x & (-x))
	int t[K];
	inline void inc(int p) {
		for (++p; p <= k + 1; p += lbt(p)) ++t[p];
	}
	inline void dec(int p) {
		for (++p; p <= k + 1; p += lbt(p)) --t[p];
	}
	inline int get(int p) {
		int r = 0;
		for (++p; p; p -= lbt(p)) r += t[p];
		return r;
	}
	inline int count(int l, int r) {
		return get(r) - get(l - 1);
	}
	#undef lbt
} // 常规树状数组，注意下标要避免为 0 

int ans = 0; // 答案 
struct edge { int to, len; };
vector<edge> G[N]; // 图 

bool centr[N]; // 重心标记 
int size[N]; // 子树大小 
int root, maxp[N]; // 重心，找重心的辅助数组 
int getSize(int x, int f) { // 计算子树大小 
	size[x] = 1;
	for (auto y : G[x])
		if (y.to != f && !centr[y.to])
			size[x] += getSize(y.to, x);
	return size[x];
}
void getCentr(int x, int f, int t) { // 找重心，其中 t 表示整个连通块的大小 
	maxp[x] = 0;
	for (auto y : G[x]) {
		if (y.to == f || centr[y.to]) continue;
		getCentr(y.to, x, t);
		maxp[x] = max(maxp[x], size[y.to]);
	}
	maxp[x] = max(maxp[x], t - size[x]);
	if (maxp[x] < maxp[root]) root = x;
}

void getPaths(int x, int f, int l, vector<int>& ds) {
	if (l > k) return; // 长度已经超过 k 的不可能成为答案，返回 
	ds.push_back(l); // 加入路径信息 
	for (auto y : G[x]) 
		if (y.to != f && !centr[y.to]) // 忽略前驱点和标记点 
			getPaths(y.to, x, l + y.len, ds); // 递归导出 
}

void solve(int x) {
	getSize(x, 0);
	maxp[root = 0] = N;
	getCentr(x, 0, size[x]);
	int s = root; // 找（分治中心）重心，现在重心为s 
	centr[s] = true; // 标记 
	
	for (auto y : G[s])
		if (!centr[y.to]) // 忽略已经被标记为重心的点
			solve(y.to); // 递归处理不经过分治中心的路径 
	
	vector<int> ds({0}); // 用于还原树状数组的暂存修改位置的数组——直接 memset 会使总复杂度变成 O(n^2) 
	bit::inc(0); // 加入根的路径信息 
	for (auto y : G[s]) {
		if (centr[y.to]) continue; // 忽略已经被标记为重心的点 
		vector<int> tds; // 该子树路径信息导出到这个数组 
		getPaths(y.to, s, y.len, tds); // 导出路径 
		for (auto i : tds) ans += bit::count(0, k - i); // 在树状数组中统计 
		for (auto i : tds) bit::inc(i); // 统计完之后将当前信息更新到树状数组中 
		ds.insert(ds.end(), tds.begin(), tds.end()); // 更新还原数组 
	}
	
	for (auto i : ds) bit::dec(i); // 逐个还原，不能直接 memset 
	centr[s] = false; // 清除重心标记 
}

signed main() {
	scanf("%d", &n);
	for (register int i = 1; i < n; i++) {
		int u, v, l;
		scanf("%d%d%d", &u, &v, &l);
		G[u].push_back(edge{v, l});
		G[v].push_back(edge{u, l});
	}
	scanf("%d", &k);
	solve(1); //开始分治 
	printf("%d
", ans);
	return 0;
}

Part 2 - 例题选讲

Part 2.1 - Luogu P4149 [IOI2011]Race

给一棵树，每条边有权。求一条简单路径，权值和等于 (k)，且边的数量最小。

(k) 的范围不是很大，所以开一个大小为 (10^6) 的桶，( ext{rec}_i) 表示权值和为 (i) 的路径的最小边数。

更具体地，假如当前重心（根）结点的所有子树的根分别为：(x_1,x_2,cdots,x_k)，而现在处理好了 (x_1,x_2,cdots,x_{k-1}) 这几颗子树之间产生的答案，那么 ( ext{rec}) 就保存了 (x_1,x_2,cdots,x_{k-1}) 这几颗子树中所有结点到根路径的信息。

对于子树 (x_k) 中某一条路径，长度和权值分别为 ((L, V))，那么这样更新答案：( ext{ans}leftarrow min( ext{ans}, ext{rec}_{k-V}+L))。

在处理完一颗子树之后，对于该子树中所有的路径，对 (rec) 这样更新：( ext{rec}_V leftarrow min( ext{rec}_V, L))。

代码：https://www.cnblogs.com/-Wallace-/p/12853760.html

• 时间复杂度：(O(nlog n))
• 空间复杂度：(O(n+k))

Part 2.2 - UVA12161 Ironman Race in Treeland

求树上的一条费用不超过 (m) 的路径,使得总长度尽量大。

考虑如何得到经过根的最优的路径。

我们一个个子结点来看，假如现在处理到子结点为 (x_k) ，那么 (x_1, x_2,cdots,x_{k-1}) 的子树已经处理完了。

现在枚举子树 (x_k) 中的所有一个端点为根的路径，当枚举到一条路径的信息为 ((D^prime, L^prime))，我们就在子树 (x_1,x_2,cdots, x_{k-1}) 中的所有路径信息中匹配——找到其中 (D) 值 (le m - D^prime) 的所有路径中 (L) 值的最大值。

这样的话，处理方式就非常多了，比较好的做法可以平衡树，但这里介绍一种虽然效率稍劣但十分简单好理解且细节极少的 动态开点线段树 做法。

回到原来那个匹配的问题：我们把前 (k-1) 个子树的路径信息存入一个动态开点线段树中，对 (D) 值域（位置）开线段树，结点维护 (L) 的最大值。那么就可以求出位置 ([0,D^prime -1]) 的最大值，然后子树 (x_k) 处理完后，在把其中的路径信息以 (D) 为位置，(L) 为值，做 单点最值操作，即 ( ext{val}_D leftarrow max( ext{val}_D, L))。还有就是记得及时清空。

这样的算法复杂度是多少呢？动态开点线段树的空间一次修改是最大多开 (log U)（(U) 为值域，下同）个结点，所以空间复杂度为 (O(nlog U))

由于深度也是最大 (log U) 层，所以时间复杂度为 (O(nlog n log U))。

代码：https://www.cnblogs.com/-Wallace-/p/12853448.html

Part 2.3 - Codeforces 715E Digit Tree

程序员 ZS 有一棵树，它可以表示为 (n) 个顶点的无向连通图，顶点编号从 (0) 到 (n-1)，它们之间有 (n-1) 条边。每条边上都有一个非零的数字。

一天，程序员 ZS 无聊，他决定研究一下这棵树的一些特性。他选择了一个十进制正整数 (M)，(gcd(M,10)=1)。

对于一对有序的不同的顶点 ((u, v))，他沿着从顶点 (u) 到顶点 (v)的最短路径，按经过顺序写下他在路径上遇到的所有数字（从左往右写），如果得到一个可以被 (M) 整除的十进制整数，那么就认为 ((u,v)) 是有趣的点对。

帮助程序员 ZS 得到有趣的对的数量。

这里采用 容斥法：即现分治中心为 (s)，当前答案等于整个子树 (s) 的答案减去以 (s) 各个子结点为根的子树的答案。

考虑如何统计。

我们设有一条路径是 (x ightarrow y)，分治中心为 (s)，路径 (x ightarrow s) 对应的数字为 (pd)，(s ightarrow y) 对应 (nd)，(s) 到 (y) 的距离为 (l)。

那么只有 (pd imes 10^l + nd equiv 0 pmod m) 成立时满足要求。

变形一下：(pd equiv -nd imes 10^{-l}pmod m)。

于是我们可以这样搞：把所有的 (pd) 用 map 存起来，记录一下个数，用 pair 数组把 ((nd, l)) 记录下来。

导入所有了路径信息后，枚举 pair 数组，查找 map 中的元素配对即可。

预处理一下 (10) 的幂及其逆元的话，时间复杂度 (O(nlog^2 n))。如果用 Hash Table 可以优化到理论 (O(nlog n)) ，但没什么必要。

代码：https://www.cnblogs.com/-Wallace-/p/12865700.html

Part 3 - 习题

• SPOJ FTOUR2 Free tour II
• Luogu P2634 [国家集训队]聪聪可可
• POJ 2114 Boatherds
• Luogu P2664 树上游戏
• Luogu P5306 [COCI2019] Transport
• BZOJ 3697 采药人的路径

Part 4 - 后记

• 原文地址：https://www.cnblogs.com/-Wallace-/p/12888265.html
• 本文作者：@-Wallace-
• 转载请附上出处。

参考资料：

• 刘汝佳 - 《算法竞赛入门经典（第2版）》 - chapter 12
• 【日】秋叶拓哉 & 岩田阳一 & 北川宜稔 - 《挑战程序设计竞赛（第2版）》 - 4.6