仪仗队这个题
理论上来说
需要使用欧拉函数
但若是将此题的正方形改为长方形
欧拉函数就不太容易使用了
当一个点的横坐标和纵坐标的 GCD 大于 1 时就会被遮挡
于是我们可以求出 横纵坐标 公约数(不是最大公约数)为 i 的个数
f[i] = (n / i) * (m / i)f[i]=(n/i)∗(m/i)
由于某些点被重复计算,我们就要去一下重
减去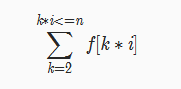
EG7ADZQW4YZNF0(7S1VHC.png)
复杂度的话是O(nlogn)的
#include<iostream> #include<cstdio> using namespace std; int py[10000002]; int main() { freopen("matrix.in","r",stdin); freopen("matrix.out","w",stdout); int n,m; ios_base::sync_with_stdio(false); cin>>n>>m; if(n==1&&m==1) { cout<<0; return 0; } if(n==1||m==1) { cout<<1; return 0; } int ans=(n-1)*(m-1); n--;m--; int l=min(n,m); for(int i=l;i>=2;i--) { py[i]=(n/i)*(m/i); for(int j=2*i;j<=l;j+=i) py[i]-=py[j]; ans-=py[i]; } cout<<ans+2; }
卡特兰数:
令h(0)=1,h(1)=1,catalan数满足递推式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
递推二式:
h(n)=h(n-1)*(4*n-2)/(n+1);
通项公式:
h(n)=(2n!)/n!*(n+1)!