P1904 天际线
题目链接:https://www.luogu.com.cn/problem/P1904
想法:
我们根据题目的意思不难发现,我们可以维护一个x轴区间对应的 y 值的最大值。然后我们去遍历我们的 x 轴对应的 y 值,如果前面一个和当前的 y 相同就说明还是直线,没有出现转折点。
但是出现了一个问题就是:为了避免边界出现问题,所以我们采取和扫描线一样的做法,让 【l,r】 代表 【l,r+1】
#include <cstdio> #include <iostream> #include <algorithm> #define ll long long #define ull unsigned long long #define ls nod<<1 #define rs (nod<<1)+1 #define pii pair<int,int> #define mp make_pair #define pb push_back #define INF 0x3f3f3f3f #define max(a, b) (a>b?a:b) #define min(a, b) (a<b?a:b) const double eps = 1e-8; const int maxn = 1e6 + 10; const ll MOD = 1e9 + 7; const int mlog=20; int sgn(double a) { return a < -eps ? -1 : a < eps ? 0 : 1; } using namespace std; struct node { int x,h,y; bool operator < (const node &a) const { return h < a.h; } }q[maxn]; int ler[maxn],x[maxn],y[maxn]; struct segment_tree { int sum; int lazy; }tree[maxn << 2]; void pushdown(int l,int r,int nod) { if (tree[nod].lazy) { tree[ls].lazy = tree[rs].lazy = tree[nod].lazy; tree[ls].sum = tree[rs].sum = tree[nod].sum; tree[nod].lazy = 0; } } void modify(int l,int r,int x,int y,int z,int nod) { if (x <= l && y >= r) { tree[nod].sum = z; tree[nod].lazy = 1; return ; } pushdown(l,r,nod); int mid = (l + r) >> 1; if (x <= mid) modify(l,mid,x,y,z,ls); if (y > mid) modify(mid+1,r,x,y,z,rs); } int query(int l,int r,int k,int nod) { if (l == r) return tree[nod].sum; int mid = (l + r) >> 1; pushdown(l,r,nod); if (k <= mid) return query(l,mid,k,ls); else return query(mid+1,r,k,rs); } int ef(int l1,int r1,int mb) { int l=l1,r=r1; while (l<=r) { int mid=(l+r)>>1; if (ler[mid]>=mb)r=mid-1; else l=mid+1; } return l; } int main() { #ifdef ONLINE_JUDGE #else freopen("/Users/ackerman/CLionProjects/codeforces/in.txt","r",stdin); #endif int m = 1; int len = 0; while (~scanf("%d%d%d",&q[m].x,&q[m].h,&q[m].y)) { ler[++len] = q[m].x; ler[++len] = q[m].y; m++; } m--; sort(ler+1,ler+1+len); sort(q+1,q+1+m); int n = 1; for (int i = 1;i < len;i++) { if (ler[i] != ler[i+1]) ler[++n] = ler[i+1]; } for (int i = 1;i <= m;i++) { q[i].x = ef(1,n,q[i].x); q[i].y = ef(1,n,q[i].y); modify(1,n,q[i].x,q[i].y-1,q[i].h,1); } for (int i = 1;i <= n;i++) { x[i] = ler[i]; y[i] = query(1,n,i,1); } for (int i = 1;i <= n;i++) { if (y[i] != y[i-1]) { printf("%d ", x[i]); printf("%d ", y[i]); } } return 0; }
P1502 窗口的星星
题目链接:https://www.luogu.com.cn/problem/P1502
想法:
因为给我们的是一个固定的矩形。我们不妨就让每一个星星其实就是一个以该星星为矩形左下角的一个固定大小的矩阵,由于边界上的星星不能算,所以我们分别把长和宽都进行-1的操作。
然后这样的话问题就转化为矩形相交的问题,我要求的就是相交的那段区间里面的最大亮度就可以了。所以问题再次转化为扫描线的思想。但是这里的话,由于我们已经对边界进行了操作所以不会出现前面一道题的边界的问题,所以我们直接正常的线段树维护就好了。
#include <cstdio> #include <iostream> #include <algorithm> #define ll long long #define ull unsigned long long #define ls nod<<1 #define rs (nod<<1)+1 #define pii pair<int,int> #define mp make_pair #define pb push_back #define INF 0x3f3f3f3f #define max(a, b) (a>b?a:b) #define min(a, b) (a<b?a:b) const double eps = 1e-8; const int maxn = 1e6 + 10; const ll MOD = 1e9 + 7; const int mlog=20; int sgn(double a) { return a < -eps ? -1 : a < eps ? 0 : 1; } using namespace std; ll x1,y1,x2,y2,X[maxn << 1]; struct ScanLine { ll l,r,h,mark; bool operator < (const ScanLine &rhs) const { if (h == rhs.h) return mark > rhs.mark; return h < rhs.h; } } line[maxn << 2]; struct segment_tree { int l,r; ll sum,lazy; }tree[maxn << 2]; void build(int l,int r,int nod) { tree[nod].l = l,tree[nod].r = r; tree[nod].lazy = 0; tree[nod].sum = 0; if (l == r) return ; int mid = (l + r) >> 1; build(l,mid,ls); build(mid+1,r,rs); } void push_up(int nod) { tree[nod].sum = max(tree[ls].sum,tree[rs].sum); } void pushdown(int nod) { if (tree[nod].lazy) { tree[ls].sum += tree[nod].lazy; tree[rs].sum += tree[nod].lazy; tree[ls].lazy += tree[nod].lazy; tree[rs].lazy += tree[nod].lazy; tree[nod].lazy = 0; } } void modify(ll x,ll y,int f,int nod) { int l = tree[nod].l,r = tree[nod].r; if (x <= l && y >= r) { tree[nod].sum += f; tree[nod].lazy += f; return ; } pushdown(nod); int mid = (l + r) >> 1; if (x <= mid) modify(x,y,f,ls); if (y > mid) modify(x,y,f,rs); push_up(nod); } int main() { int t; scanf("%d",&t); while (t--) { ll n,w,h; scanf("%lld%lld%lld",&n,&w,&h); for (int i = 1;i <= n;i++) { ll x,y,l; scanf("%lld%lld%lld",&x,&y,&l); X[2 * i - 1] = x; X[2 * i] = x + w - 1; line[2 * i - 1] = {x,x+w-1,y,l}; line[2 * i] = {x,x+w-1,y+h-1,-l}; } n <<= 1; sort(X + 1,X + 1 + n); sort(line + 1,line + 1 + n); ll tot = unique(X + 1,X + 1 + n) - X - 1; build(1,tot,1); ll ans = 0; for (int i = 1;i <= n;i++) { ll l = upper_bound(X + 1,X + 1 + tot,line[i].l) - X - 1; ll r = upper_bound(X + 1,X + 1 + tot,line[i].r) - X - 1; modify(l,r,line[i].mark,1); ans = max(ans,tree[1].sum); } printf("%lld ",ans); } return 0; }
P5816 [CQOI2010]内部白点
题目链接:https://www.luogu.com.cn/problem/P5816
想法:
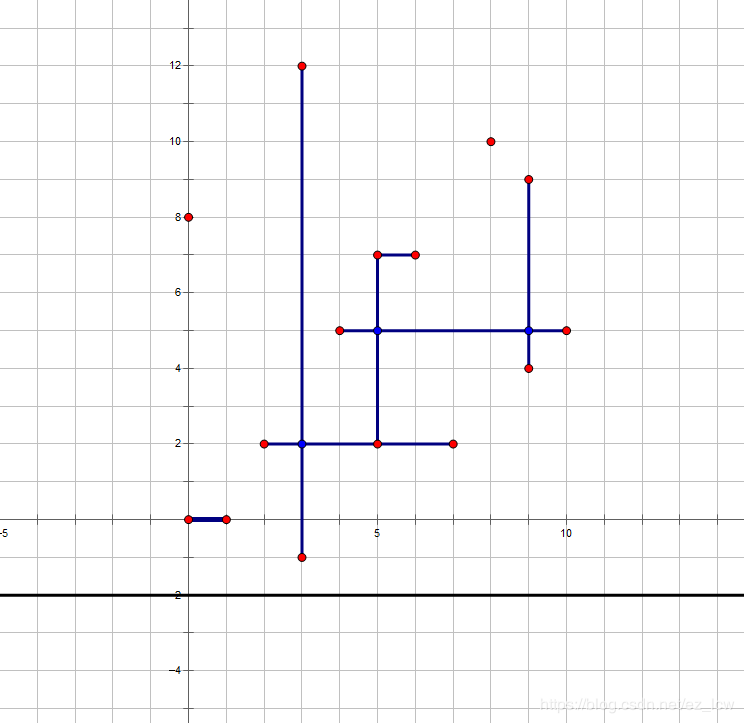
(图来自ez_lcw)
只有水平线和垂直线才会对白点的出现产生影响,所以我们可以维护这两种的线段。
如果出现了水平线,我们就查询这段区间。 如果出现了垂线,下端点我们让他+1,上端点我们让他-1
然后按照 y 的顺序对这些线段进行排序。
#include <cstdio> #include <iostream> #include <algorithm> #define ll long long #define ull unsigned long long #define ls nod<<1 #define rs (nod<<1)+1 #define pii pair<int,int> #define mp make_pair #define pb push_back #define INF 0x3f3f3f3f #define max(a, b) (a>b?a:b) #define min(a, b) (a<b?a:b) const double eps = 1e-8; const int maxn = 1e5 + 10; const ll MOD = 1e9 + 7; const int mlog=20; int sgn(double a) { return a < -eps ? -1 : a < eps ? 0 : 1; } using namespace std; struct BIT { ll c[maxn << 2]; int n; void init(int sz) {n=sz;for(int i = 0;i <= n+1;i++) c[i]=0;} ll qwq(int x) { ll ans=0; for(;x;x-=x&-x) ans+=c[x]; return ans; } ll qry(int l,int r) {return qwq(r)-qwq(l-1);} void upd(int x,ll v=1) {if(x!=0) for(;x<=n;x+=x&-x) c[x]+=v;} }bit; struct ScanLine { ll l,r,h; int mark; bool operator < (const ScanLine &rhs) const { if (h == rhs.h) return mark < rhs.mark; return h < rhs.h; } } line[maxn << 2]; struct node { int x,y; }p[maxn]; int x[maxn]; bool cmpx(node a,node b) { if (a.x == b.x) return a.y < b.y; return a.x < b.x; } bool cmpy(node a,node b) { if (a.y == b.y) return a.x < b.x; return a.y < b.y; } int main() { int n; scanf("%d",&n); for (int i = 1;i <= n;i++) { scanf("%d%d",&p[i].x,&p[i].y); x[i] = p[i].x; } sort(x+1,x+1+n); int tot = unique(x+1,x+1+n) - x - 1; bit.init(tot); for (int i = 1;i <= n;i++) { p[i].x = lower_bound(x+1,x+tot+1,p[i].x) - x; } sort(p+1,p+1+n,cmpx); int cnt = 0; for (int i = 1;i < n;i++) { if (p[i].x == p[i+1].x) { line[++cnt] = {p[i].x,0,p[i].y,1}; line[++cnt] = {p[i].x,0,p[i+1].y,-1}; } } sort(p+1,p+1+n,cmpy); for (int i = 1;i < n;i++) { if (p[i].y == p[i+1].y) { line[++cnt] = {p[i].x,p[i+1].x,p[i].y,0}; } } sort(line+1,line+1+cnt); int ans = 0; for (int i = 1;i <= cnt;i++) { if (!line[i].mark) ans += bit.qry(line[i].l,line[i].r); else bit.upd(line[i].l,line[i].mark); } printf("%d ",ans + n); return 0; }