二维ST表
既然查询对象是个二维矩阵,那么我们能不能维护一个二维的ST STST表呢?答案显然是肯定的。
预处理:
我们让 dp[i][j][k][l] 为新的ST表,表示以 (i,j) 为左上角,右下角为 (i + 2^k -1 , j + 2^l - 1) 的矩阵中的最大值,那么我们可以看出预处理的复杂度是O(nmlognlogm)
我们来看对于每一个dp[i][j][k][l] 可以又哪些状态更新:
下图是一个矩阵:
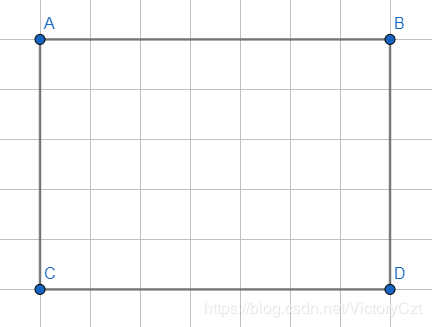
我们假设这个矩阵的左上角是 (i,j) 右下角是 (i + 2^k - 1,j + 2^l - 1)
我们把这个矩阵分成两个部分:


查询:
对于一个子矩阵,我们假设它的左上角的坐标为 (x1,y1) , 右下角为 (x2,y2) 那么可以通过预处理得到二维ST表,将其分为四部分查询

1 #include<iostream> 2 #include<cstdio> 3 #include<string.h> 4 #include<string> 5 #include<stack> 6 #include<set> 7 #include<algorithm> 8 #include<cmath> 9 #include<vector> 10 #include<map> 11 12 13 #define ll __int64 14 #define lll unsigned long long 15 #define MAX 1000009 16 #define eps 1e-8 17 18 using namespace std; 19 /* 20 二维RMQ模板题 21 同一维一样 用dp[row][col][i][j]表示(row,col)到(row+2^i,col+2^j)矩形内的最小值 22 查询 23 */ 24 25 int mapp[309][309]; 26 int dp[309][309][9][9]; 27 int flag; 28 29 void RMQ_init2d(int m,int n) 30 { 31 for(int i=1; i<=m; i++) 32 { 33 for(int j = 1; j<=n; j++) 34 { 35 dp[i][j][0][0] = mapp[i][j]; 36 } 37 } 38 int t = log((double)n) / log(2.0); 39 40 for(int i = 0; i<=t; i++) 41 { 42 for(int j = 0; j<=t; j++) 43 { 44 if(i==0&&j==0) 45 continue; 46 for(int row = 1; row+(1<<i)-1<= m; row++) 47 { 48 for(int col = 1; col+(1<<j)-1<= n; col++) 49 { 50 if(i) 51 dp[row][col][i][j] = max(dp[row][col][i-1][j],dp[row+(1<<(i-1))][col][i-1][j]); 52 else 53 dp[row][col][i][j] = max(dp[row][col][i][j-1],dp[row][col+(1<<(j-1))][i][j-1]); 54 } 55 } 56 } 57 } 58 } 59 int RMQ_2d(int x1,int y1,int x2,int y2) 60 { 61 int k1 = log(double(x2 - x1 + 1)) / log(2.0); 62 int k2 = log(double(y2 - y1 + 1)) / log(2.0); 63 int m1 = dp[x1][y1][k1][k2]; 64 int m2 = dp[x2 - (1<<k1) + 1][y1][k1][k2]; 65 int m3 = dp[x1][y2 - (1<<k2) + 1][k1][k2]; 66 int m4 = dp[x2 - (1<<k1) + 1][y2 - (1<<k2) + 1 ][k1][k2]; 67 int _max = max(max(m1,m2),max(m3,m4)); 68 if(mapp[x1][y1]==_max||mapp[x1][y2]==_max||mapp[x2][y1]==_max||mapp[x2][y2]==_max) 69 flag = 1; 70 return _max; 71 } 72 73 int main() 74 { 75 int n,m,t; 76 int x1,x2,y1,y2; 77 while(~scanf("%d%d",&m,&n)) 78 { 79 for(int i = 1; i<=m; i++) 80 { 81 for(int j = 1; j<=n; j++) 82 { 83 scanf("%d",&mapp[i][j]); 84 } 85 } 86 RMQ_init2d(m,n); 87 scanf("%d",&t); 88 while(t--) 89 { 90 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 91 92 flag = 0; 93 int _max = RMQ_2d(x1,y1,x2,y2); 94 if(flag == 1) 95 printf("%d yes ",_max); 96 else 97 printf("%d no ",_max); 98 } 99 } 100 return 0; 101 }