线段树基础

1|0浅谈线段树

线段树个人理解和运用时，认为这个是一个比较实用的优化算法。
这个东西和区间树有点相似，是一棵二叉搜索树，也就是查找节点和节点所带值的一种算法。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)，这个时间复杂度非常的理想，但是空间复杂度在应用时是开4N的。
所以这个算法有优势，也有劣势。

1|1我们提出一个问题

如果当前有一个区间，需要你在给定区间内做以下操作：

l,z 在l上加上z
l 查询l的值
l,r,z 在[l,r]区间所有数都+z
l,r, 查询l到r之间的和
你是不是在想，暴力解决一切问题，但是如果给你的数据是极大的，暴力完全做不了。
那么我们就需要使用线段树了。

|2线段树的一些基本操作

建树
单点修改
单点查找
区间修改
区间查找
pushup（儿子把信息传给父亲）
pushdown（父亲把信息传给儿子）
（其他的应该都是这些基本操作的变形）
以下我们来逐一讲解一下

1|3结构体

作为一课非常正经的树，我们还是要给它开一个结构体。

struct segment_tree{
    int l,r,sum;
}tree[MAXN];

1|4关于线段树的一些小提醒

我们写线段树，应该先知道当前节点nod的左右儿子的编号是多少，答案是(nod2)和(nod2+1)
为什么？我们写的线段树应该是一棵满二叉树，所以根据满二叉树节点的特点，我们就可以知道了他的儿子就是以上的答案。

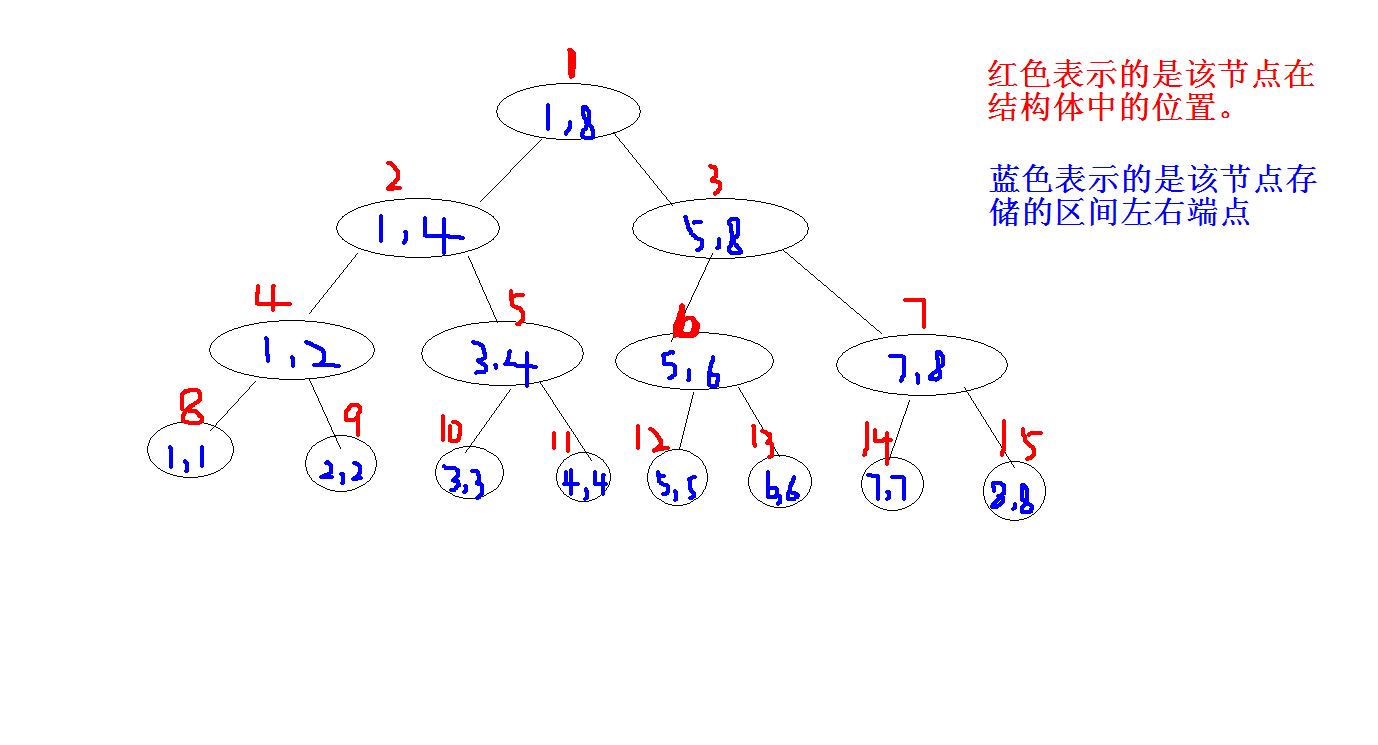
线段树的建立我们不妨可以理解成：

先找到叶子节点，然后递归回溯到它的父亲节点，建立父亲节点的左右孩子。

 1 void build(int l,int r,int nod)
 2 {
 3     if (l == r)
 4     {
 5         tree[nod].l = l;
 6         tree[nod].r = r;
 7         tree[nod].sum = a[l];
 8     }
 9     int mid = (l+r)>>1;
10     build(l,mid,nod<<1);
11     build(mid+1,r,(nod<<1)+1);
12     pushup(nod);
13 }

有人在问这个pushup是什么东西？

1|6pushup

pushup就是把儿子的信息上传给自己的父亲节点，也就是左右孩子建立完后，我们要更新父亲节点
以当前问题为例，那么这个pushup的过程就是以下程序

1 void pushup(int nod)
2 {
3     tree[nod].sum = tree[nod<<1].sum + tree[(nod<<1)+1].sum;
4 }

1|7单点修改

我们单点修改只需要直接在原节点上修改就可以了。
那么我们废话不多说，直接上代码更好理解

k代表我们修改的点的位置

void update_first(int l,int r,int k,int value,int nod)
{
    if (l == r)
    {
        tree[nod].sum += value;   // 这里可以根据题目的要求而进行修改
        return ;
    }
    int mid = (l+r)>>1;
    if (k<=mid)
        update_first(l,mid,k,value,nod<<1);
    else
        update_first(mid+1,r,k,value,(nod<<1)+1);
    pushup(nod);
}

提醒一下：修改完孩子节点之后，我们一定要去更新父亲节点！

1|8单点查找

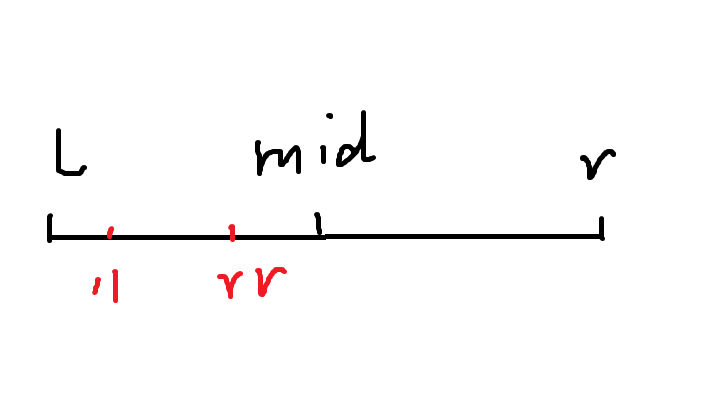
方法与二分查询基本一致，如果当前枚举的点左右端点相等，即叶子节点，就是目标节点。如果不是，因为这是二分法,所以设查询位置为x，当前结点区间范围为了l，r，中点为mid，则如果x<=mid，则递归它的左孩子，否则递归它的右孩子。
直接上代码

int query_first(int l,int r,int ll,int rr,int nod)
{
    if (l == ll && r == rr)
    {
        return tree[nod].sum;
    }
    int mid = (l+r)>>1;
    if (rr<=mid)
        return query_first(l,mid,ll,rr,nod<<1);
    else if (ll > mid)
        return query_first(mid+1,r,ll,rr,(nod<<1)+1);
    else
        return query_first(l,mid,ll,mid,nod<<1)+query_first(mid+1,r,mid+1,rr,(nod<<1)+1);
}

1|9区间修改

我们思考一个问题，如果我们只是像单点修改那样子，用一个循环语句，把要修改区间内的所有点都进行单点修改，那么这个的复杂度应该是O(NlogN)，那么这就无法发挥出线段树的优势了。
那么我们应该怎么做呢？
这个时候我们就需要引入一个叫做懒标记的东西。
顾名思义，这个就是一个非常懒的标记，这个就是在我们要的区间内的节点上所加的标记，这个标记也就只有我们要对父亲区间内的数进行修改或者附其他值的时候才会用到的一个东西。

这个标记比较难理解，所以我们稍微讲的详细一点？

通俗来说的话就是我只在我要修改的那个区间进行标记，如果你要去查找的是我修改这个区间的左右孩子，那么就需要去pushdown懒惰标记。

 1 void update_second(int l,int r,int ll,int rr,int value,int nod)
 2 {
 3     if (l == ll && r == rr)
 4     {
 5         tree[nod].sum += (r-l+1)*value;
 6         tree[nod].lazy += value;
 7         return ;
 8     }
 9     pushdown(nod,l,r);
10     int mid = (l+r)>>1;
11     if (rr<=mid)
12         update_second(l,mid,ll,rr,value,nod<<1);
13     else if (ll>mid)
14         update_second(mid+1,r,ll,rr,value,(nod<<1)+1);
15     else{
16         update_second(l,mid,ll,mid,value,nod<<1);
17         update_second(mid+1,r,mid+1,rr,value,(nod<<1)+1);
18     }
19     pushup(nod);
20 }

我们再回到这个问题，为什么会有这么多的if语句，我们现在来讲解一下
ll，rr是需要修改的区间。
当你的区间的rr也就是最右边在mid的左边，那么说明我们整个区间就在l和mid之间，就是以下的情况

好了右区间也是一样，其他的情况就是当前的区间分布在mid的左右，那么就分成两部分修改就可以了
那么最后因为儿子可能被改变了，所以我们就要pushup一下。

1|10pushdown

这个操作在上文已经讲过是把父亲的lazy下传给儿子的过程。
直接上代码

void pushdown(int nod,int l,int r)
{
    if (tree[nod].lazy)
    {
        int mid = (l+r)>>1;
        tree[nod<<1].sum += (mid-l+1)*tree[nod].lazy;
        tree[(nod<<1)+1].sum += (r-mid)*tree[nod].lazy;
        tree[nod<<1].lazy += tree[nod].lazy;
        tree[(nod<<1)+1].lazy += tree[nod].lazy;
        tree[nod].lazy = 0;
    }

}

1|11区间查询

这个道理和区间修改差不多，还更简单一点。
也不多讲了，直接上代码

int query_second(int l,int r,int ll,int rr,int nod)
{
    if (l == ll && r == rr)
        return tree[nod].sum;
    pushdown(nod,l,r);
    int mid = (l+r)>>1;
    if (rr<=mid)
        return query_second(l,mid,ll,rr,nod<<1);
    else if (ll>mid)
        return query_second(mid+1,r,ll,rr,(nod<<1)+1);
    else{
        return query_second(l,mid,ll,mid,nod<<1)+query_second(mid+1,r,mid+1,rr,(nod<<1)+1);
    }
}

检测板子的地方：https://www.luogu.org/problem/P3372

板子：

  1 #include <stdio.h>
  2 #include <algorithm>
  3 #include <iostream>
  4 #include <stdbool.h>
  5 #include <stdlib.h>
  6 #include <string>
  7 #include <string.h>
  8 #include <stack>
  9 #include <map>
 10 
 11 #define INF 0x3f3f3f3f
 12 #define LL long long
 13 using namespace std;
 14 const int MAXN = 2e5+5;
 15 
 16 struct segment_tree{
 17     LL l,r,sum;
 18     LL lazy;
 19 }tree[(MAXN<<2)+10];
 20 
 21 LL a[MAXN<<2];
 22 
 23 void pushup(LL nod)
 24 {
 25     tree[nod].sum = tree[nod<<1].sum + tree[(nod<<1)+1].sum;
 26 }
 27 
 28 void pushdown(LL l,LL r,LL nod)
 29 {
 30     if (tree[nod].lazy) {
 31         LL mid = (l + r) >> 1;
 32         tree[nod << 1].sum += (mid - l + 1) * tree[nod].lazy;
 33         tree[(nod << 1) + 1].sum += (r - mid) * tree[nod].lazy;
 34         tree[nod << 1].lazy += tree[nod].lazy;
 35         tree[(nod << 1) + 1].lazy += tree[nod].lazy;
 36         tree[nod].lazy = 0;
 37     }
 38 }
 39 void build(LL l,LL r,LL nod)
 40 {
 41     if (l == r)
 42     {
 43         tree[nod].sum = a[l];
 44         tree[nod].l = l;
 45         tree[nod].r = r;
 46         tree[nod].lazy = 0;
 47         return ;
 48     }
 49     LL mid = (l+r)>>1;
 50     build(l,mid,nod<<1);
 51     build(mid+1,r,(nod<<1)+1);
 52     pushup(nod);
 53 }
 54 
 55 void update_second(LL l,LL r,LL ll,LL rr,LL nod,LL value)
 56 {
 57     if (l == ll && r == rr)
 58     {
 59         tree[nod].sum += (r-l+1)*value;
 60         tree[nod].lazy += value;
 61         return ;
 62     }
 63     pushdown(l,r,nod);
 64     LL mid = (l+r)>>1;
 65     if (rr<=mid)
 66         update_second(l,mid,ll,rr,nod<<1,value);
 67     else if (ll>mid)
 68         update_second(mid+1,r,ll,rr,(nod<<1)+1,value);
 69     else{
 70         update_second(l,mid,ll,mid,nod<<1,value);
 71         update_second(mid+1,r,mid+1,rr,(nod<<1)+1,value);
 72     }
 73     pushup(nod);
 74 }
 75 
 76 LL query_second(LL l,LL r,LL ll,LL rr,LL nod)
 77 {
 78     if (l == ll && r == rr)
 79         return tree[nod].sum;
 80     pushdown(l,r,nod);
 81     LL mid = (l+r)>>1;
 82     if (rr<=mid)
 83         return query_second(l,mid,ll,rr,nod<<1);
 84     else if (ll>mid)
 85         return query_second(mid+1,r,ll,rr,(nod<<1)+1);
 86     else
 87         return query_second(l,mid,ll,mid,nod<<1)+query_second(mid+1,r,mid+1,rr,(nod<<1)+1);
 88 }
 89 
 90 int main()
 91 {
 92     LL n,m;
 93     scanf("%lld%lld",&n,&m);
 94     for (int i=1;i<=n;i++)
 95         scanf("%lld",&a[i]);
 96     build(1,n,1);
 97     while (m--)
 98     {
 99         LL x,y,z,k;
100         scanf("%lld",&x);
101         if (x == 1)
102         {
103             scanf("%lld%lld%lld",&y,&z,&k);
104             update_second(1,n,y,z,1,k);
105         }
106         else
107         {
108             scanf("%lld%lld",&x,&y);
109             printf("%lld
",query_second(1,n,x,y,1));
110         }
111     }
112     return 0;
113 }

感谢大佬博客让我弄懂了基础的线段树：https://www.cnblogs.com/Dawn-Star/p/9678198.html#autoid-1-1-0

-------------------------------------------------------------------------------------------------------------

线段树模版 (区间修改 + 求区间最大值/最小值)

  1 #include <stdio.h>
  2 #include <algorithm>
  3 #include <iostream>
  4 #include <stdbool.h>
  5 #include <stdlib.h>
  6 #include <string>
  7 #include <string.h>
  8 #include <stack>
  9 #include <queue>
 10 #include <set>
 11 #include <map>
 12 #include <math.h>
 13 
 14 #define INF 0x3f3f3f3f
 15 #define LL long long
 16 using namespace std;
 17 
 18 const int maxn = 100050;
 19 
 20 int w[maxn];
 21 
 22 
 23 struct segment_tree{
 24     int l,r;
 25     LL val;
 26     LL maxval;
 27     int lazy;
 28 }tree[maxn*4];
 29 
 30 void pushup(int nod){
 31     tree[nod].val = (tree[nod<<1].val + tree[(nod<<1)+1].val);
 32     tree[nod].maxval = max(tree[nod<<1].maxval,tree[(nod<<1)+1].maxval);
 33 }
 34 
 35 void pushdown(int nod){
 36     tree[nod<<1].lazy += tree[nod].lazy;
 37     tree[(nod<<1)+1].lazy += tree[nod].lazy;
 38     tree[nod<<1].val += (tree[nod<<1].r-tree[nod<<1].l + 1) * tree[nod].lazy;
 39     tree[(nod<<1)+1].val += (tree[(nod<<1)+1].r-tree[(nod<<1)+1].l+1) * tree[nod].lazy;
 40     tree[nod<<1].maxval += tree[nod].lazy;
 41     tree[(nod<<1)+1].maxval += tree[nod].lazy;
 42     tree[nod].lazy = 0;
 43 }
 44 
 45 void build (int l,int r,int nod){
 46     tree[nod].l = l;
 47     tree[nod].r = r;
 48     if (l == r){
 49         tree[nod].lazy = 0;
 50         tree[nod].val = w[l];
 51         tree[nod].maxval = w[l];
 52         return ;
 53     }
 54     int mid = (l + r) >> 1;
 55     build(l,mid,nod<<1);
 56     build(mid+1,r,(nod<<1)+1);
 57     pushup(nod);
 58 }
 59 
 60 
 61 void modify(int x,int y,int z,int k=1){
 62     int l = tree[k].l, r = tree[k].r;
 63     if (x <= l && y>=r){
 64         tree[k].lazy += z;
 65         tree[k].val += (r-l+1) * z;
 66         tree[k].maxval += z;
 67         return ;
 68     }
 69     if (tree[k].lazy){
 70         pushdown(k);
 71     }
 72     int mid = (l + r) >> 1;
 73     if (x <= mid){
 74         modify(x,y,z,k<<1);
 75     }
 76     if (y > mid){
 77         modify(x,y,z,(k<<1)+1);
 78     }
 79     pushup(k);
 80 }
 81 
 82 LL query(int x,int y,int k=1){
 83     int l = tree[k].l,r = tree[k].r;
 84     if (x <= l && y >= r){
 85         return tree[k].val;
 86     }
 87     if (tree[k].lazy){
 88         pushdown(k);
 89     }
 90     int mid = (l + r) >> 1;
 91     LL sum = 0;
 92     if (x <= mid){
 93         sum += query(x,y,k<<1);
 94     }
 95     if (y > mid){
 96         sum += query(x,y,(k<<1)+1);
 97     }
 98     return sum;
 99 }
100 
101 LL query2(int x,int y,int k=1){
102     int l = tree[k].l,r = tree[k].r;
103     if (x <= l && y >= r){
104         return tree[k].maxval;
105     }
106     if (tree[k].lazy){
107         pushdown(k);
108     }
109     int mid = (l + r) >> 1;
110     LL sum = 0;
111     if (x <= mid){
112         sum = max(sum,query2(x,y,k<<1));
113     }
114     if (y > mid){
115         sum = max(query2(x,y,(k<<1)+1),sum);
116     }
117     return sum;
118 }
119 
120 int main(){
121     int n;
122     scanf("%d",&n);
123     for (int i=1;i<=n;i++){
124         scanf("%d",&w[i]);
125     }
126     build(1,n,1);
127     modify(1,4,3);
128     printf("%lld
 %lld",query2(1,5),query(1,5));
129     return 0;
130 }

线段树模版（单点修改 + 区间查询）

struct segment_tree {
    LL val;
}tree[maxn << 2];
int q[maxn];

void build (int l,int r,int nod) {
    if (l == r) {
        tree[nod].val = q[l];
        return ;
    }
    int mid = (l + r ) >> 1;
    build(l,mid,ls);
    build(mid+1,r,rs);
    tree[nod].val = (tree[ls].val + tree[rs].val) % mod;
}

void modify(int l,int r,int k,LL v,int nod) {
    if (l == r) {
        tree[nod].val = v;
        return ;
    }
    int mid = (l + r) >> 1;
    if (k <= mid)
        modify(l,mid,k,v,ls);
    else
        modify(mid+1,r,k,v,rs);
    tree[nod].val = (tree[ls].val + tree[rs].val) % mod;
}


LL query(int l,int r,int ql,int qr,int nod) {
    if (ql <= l && qr >= r)
        return tree[nod].val;
    int mid = (l + r ) >> 1;
    if (ql <= mid)
        return query(l,mid,ql,qr,ls);
    if (qr > mid)
        return query(mid+1,r,ql,qr,rs);
    return (query(l,mid,ql,qr,ls)%mod+query(mid+1,r,ql,qr,rs)%mod)%mod;
}

相关阅读:
STM32 ~ 查看系统时钟
 Allegro从.brd文件中导出器件封装
 Cadence原理图与Allegro交互
 Cadence关闭StartPage的方法
 emWin 移植
 python闭包
 python多线程之threading
3.1决策树算法应用
 3.1决策树算法
 MyEclipse10 配置python的pyDev
原文地址：https://www.cnblogs.com/-Ackerman/p/11250958.html