HDU-4190-Number Sequence-容斥原理+多重集和的r组合
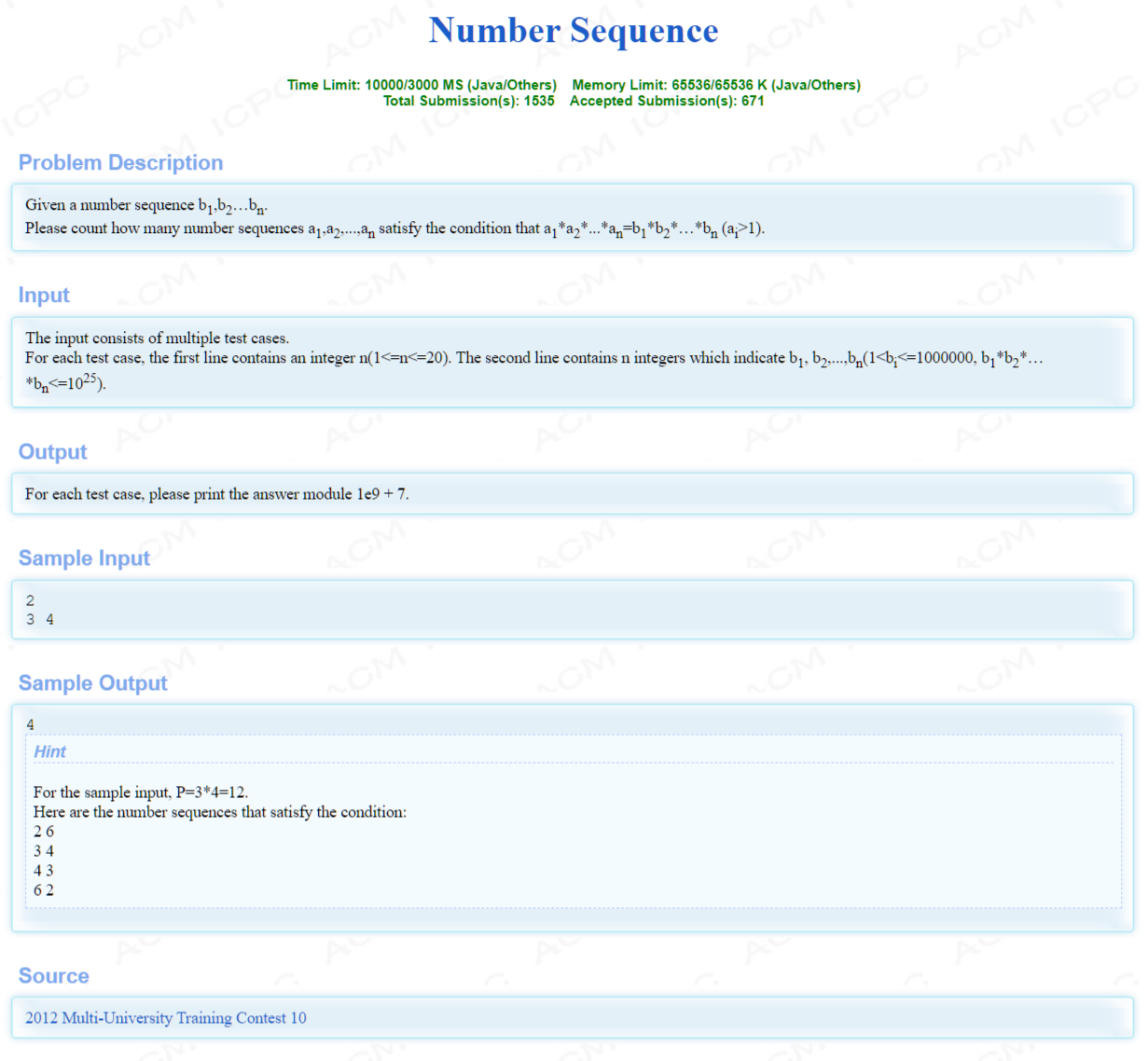
【Problem Description】
给你(n)个数(b_i),问有多少个长度为(n)序列(a_i),使得(a_1cdot a_2dots a_n=b_1cdot b_2dots b_n)。且(a_i>1)。
【Solution】
将所有(b_i)分解质因数,并分别统计每个质因数出现的次数,那么可以肯定,所有的(a_i)一定是从这些质因数中选取不同的组合相乘得到的。
假设没有(a_i>1)的限制,然后假设所有的(b_i)共有(3)个质因子,每个质因子出现的次数分别为(a,b,c)次。则总共有({a+n-1choose n-1}cdot {b+n-1choose n-1}cdot {c+n-1choose n-1})种长度为(n)的(a_i)序列。即类似总共有(n)个不同的盒子,将(a)个红球,(b)个蓝球,(c)个绿球放进这(n)个盒子中有多少种不同的方案,可以使得。
但是现在求得的答案数包括了(a_i=1)的情况,需要去除,即减去(1)个位置为空的方案数,再加上(2)个位置为空的方案数,再减去(dots)等等。(i)个位置为空的方案数为({nchoose i}cdot {a+n-1-ichoose n-1-i}cdot {b+n-1-ichoose n-1-i}cdot {c+n-1-ichoose n-1-i})。即先从(n)个盒子种选(i)个位置,有({nchoose i})种方案,然后再乘以将(a)个红球,(b)个蓝球,(c)个绿球放进(n-i)个盒子中的方案数。
【Code】
#include<iostream>
#include<algorithm>
#include<map>
#include<cstring>
#include<cstdio>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 1000005
#define int long long
const int mod=1e9+7;
int a[25];
int prime[maxn],cnt=0;
bool vis[maxn]={1,1};
void Euler(){ //欧拉筛
for(int i=2;i<maxn;i++){
if(!vis[i]) prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
map<int,int>mp; //统计每个质因数出现的次数
void solve(int n){ //求质因数
for(int i=1;i<=cnt&&prime[i]*prime[i]<=n;i++){
int p=prime[i],num=0;
if(n%p==0){
while(n%p==0) n/=p,num++;
mp[p]+=num;
}
}
if(n>1) mp[n]++;
}
int C[105][105]; //组合数
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);Euler();
for(int i=0;i<105;i++) C[i][0]=1;
for(int i=1;i<105;i++){ //预处理组合数
for(int j=1;j<=i;j++){
C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
}
int n;
while(cin>>n){
mp.clear();
for(int i=1;i<=n;i++) cin>>a[i],solve(a[i]);
int ans=1;
for(auto v:mp){ //求出ai没有限制时的方案数
ans=(ans*C[v.second+n-1][n-1])%mod;
}
for(int i=1;i<n;i++){ //容斥减去ai=1的方案
int tmp=C[n][i];
for(auto v:mp){
tmp=tmp*C[v.second+n-1-i][n-1-i]%mod;
}
ans=(ans+(i&1?-1:1)*tmp)%mod;
}
cout<<(ans+mod)%mod<<endl;
}
return 0;
}