ZOJ

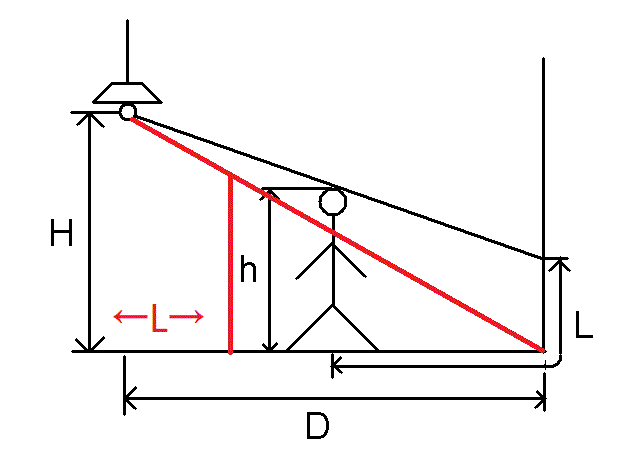
题意：灯离地面的高度为$H$，人的身高为$h$，灯离墙的距离为$D$，人站在不同位置，影子的长度不一样，求出影子的最长长度。

思路：设人离灯的距离为$x$，当人走到距离灯长度为$L$时，人在墙上的影子消失，此时人再往前走，影子的长度必然会减小，此时的$L$就为三分的左边界，右边界为$R=D$，由形似三角形可以推导出$L=D-frac{h*D}{H}$，影子的长度

$$f(x)=D-x+H-frac{(H-h)*D}{x},xin [D-frac{h*D}{H},D]$$

在区间$[D-frac{h*D}{H},D]$三分求极值即可。

#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const double eps = 1e-5;

int t;
double H, h, D;

double f(double x)
{
    return D - x + H - (H - h) * D / x;
}

double three_devide(double l, double r)
{
    while (r - l > eps) {
        double lmid = (l + r) / 2;
        double rmid = (lmid + r) / 2;
        if (f(lmid) < f(rmid)) l = lmid;
        else r = rmid;
    }
    return l;
}

int main()
{
    scanf("%d", &t);
    while (t--) {
        scanf("%lf%lf%lf", &H, &h, &D);
        double res = f(three_devide(D - h * D / H, D));
        printf("%.3lf
", res);
    }
    return 0;
}

记录一下三分的模板：

求单峰函数的极值时，如果$f(lmid)<f(rmid)$，则令$l=lmid$，否则令$r=rmid$

求单谷函数的极值时，如果$f(lmid)>f(rmid)$，则令$l=lmid$，否则令$r=rmid$