题意:给你一张无向连通图,对于求有多少对$(x,y)$满足互相到达必须经过$(a,b)$,其中$x eq a,x eq b,y eq a,y eq b$
思路:显然$a,b$都必须为割点,所以先用$tarjan$判断$a,b$是否都为割点,如果$a$或$b$有一个不为割点,那么答案就是$0$
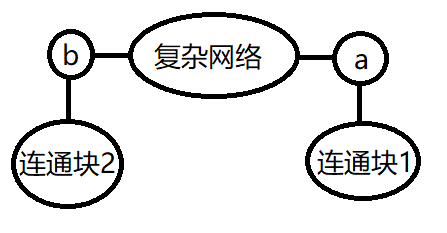
当$a,b$都为割点时,答案为连通块$1$内点的个数$*$连通块$2$内点的个数,以求连通块$1$内点的个数为例,从$b$点开始$dfs$,当遇到$a$点时停止,统计出$($连通块$2+$复杂网络$+b+a)$这些点的个数,连通块$1$内点的个数就是用$n$减去$dfs$求出的点的个数,求连通块$2$内点的个数从$a$点开始$dfs$即可。
#include <iostream> #include <algorithm> #include <cstdio> using namespace std; const int N = 500010; typedef long long ll; struct node { int to, nex; }; node edge[2 * N]; int t, n, m, a, b, cnt, head[N]; int dfn[N], timing, pcut[N]; int cnta, cntb, vis[N]; void dfs(int u, int mk, int a, int b) { vis[u] = 1; if (0 == mk) cnta++; if (1 == mk) cntb++; if (0 == mk && u == b) return; if (1 == mk && u == a) return; for (int i = head[u]; 0 != i; i = edge[i].nex) { int v = edge[i].to; if (!vis[v]) dfs(v, mk, a, b); } return; } void add_edge(int u, int v) { edge[++cnt].to = v; edge[cnt].nex = head[u]; head[u] = cnt; } int tarjan(int u, int fa) { int child = 0, lowu; lowu = dfn[u] = ++timing; for (int i = head[u]; 0 != i; i = edge[i].nex) { int v = edge[i].to; if (!dfn[v]) { child++; int lowv = tarjan(v, u); if (lowv >= dfn[u] && u != fa) pcut[u] = 1; lowu = min(lowu, lowv); } else if (v != fa) { lowu = min(lowu, dfn[v]); } } if (u == fa && child > 1) pcut[u] = 1; return lowu; } void init() { cnt = timing = cnta = cntb = 0; for (int i = 1; i <= n; i++) pcut[i] = dfn[i] = head[i] = 0; } int main() { scanf("%d", &t); while (t--) { scanf("%d%d%d%d", &n, &m, &a, &b); init(); for (int i = 1; i <= m; i++) { int u, v; scanf("%d%d", &u, &v); add_edge(u, v), add_edge(v, u); } for (int i = 1; i <= n; i++) { if (0 == dfn[i]) tarjan(i, i); } if (0 == pcut[a] || 0 == pcut[b]) { printf("0 "); continue; } for (int i = 1; i <= n; i++) vis[i] = 0; dfs(a, 0, a, b); for (int i = 1; i <= n; i++) vis[i] = 0; dfs(b, 1, a, b); ll x = ll(n - cnta), y = ll(n - cntb); printf("%lld ", x * y); } return 0; }