参考链接:https://blog.csdn.net/walilk/article/details/78175912
稀疏编码与PCA的区别:
回顾一下PCA:
1. 原数据点与投影点距离最小化 ==> 协方差最大化
2. 奇异值分解得到完备基(PCA的关键)
稀疏编码与PCA不同,它得到的是超完备基,即向量基的个数比最大无关向量组多。但是多多少呢??
PCA得到的是完备基,因此系数向量是唯一的;但是超完备基的系数向量不唯一。
那么如何得到超完备基呢??
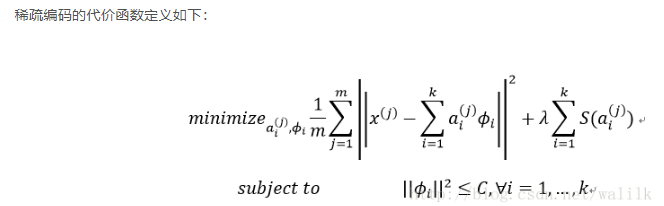
上式前一项与PCA一样,都是距离最小化,但是多了第二项的“稀疏性惩罚”,用范数来表示。这样既保证了拟合效果,又考虑了稀疏性。
为了防止a过小,才有约束条件Φ<C。
k>n,k是如何确定的?


稀疏的概念:
这里把“稀疏性(sparsity )”定义为:只有很少的几个非零元素或只有很少的几个远大于零的元素。
要求系数向量 a 是稀疏的意思就是说:对于一个输入向量的基向量组合,我们只想有尽可能少的几个系数远大于零。
范数和稀疏的关系:
用范数来表示稀疏性。
稀疏编码是无监督学习!