Error Probability Bounds for Convolutional Codes
Finding bounds on the error performance of convolutional codes is different from the
method used to find error bounds for block codes because here we are dealing with
sequences of very large length; because the free distance of these codes is usually
small, some errors will eventually occur. The number of errors is a random variable
that depends on both the channel characteristics (signal-to-noise ratio in soft-decision
decoding and crossover probability in hard-decision decoding) and the length of the
input sequence. The longer the input sequence, the higher the probability of making
errors. Therefore, it makes sense to normalize the number of bit errors to the length of
the input sequence. A measure that is usually adopted for comparing the performance
of convolutional codes is the expected number of bits received in error per input bit. To
find a bound on the average number of bits in error for each input bit, we first derive a
bound on the average number of bits in error for each input sequence of length k. To
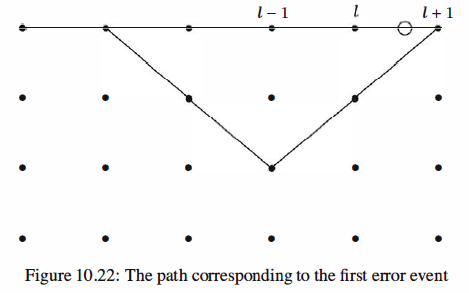
determine this, let us assume that the all-0 sequence is transmitted and, up to stage l
in the decoding, there has been no error. Now k information bits enter the encoder and
result in moving to the next stage in the trellis. We are interested in finding a bound
on the expected number of errors that can occur due to this input block of length k.
Because we are assuming that up to stage l there has been no error, up to this stage the
all-0 path through the trellis has the minimum metric. Now, as we move to the next
stage [stage ( l + 1) st] it is possible that another path through the trellis will have a
metric less than the all-0 path and therefore cause errors. If this happens, we must have
a path through the trellis that merges with the all-0 path for the first time at the (l + 1 )st
stage and has a metric less than the all-0 path. Such an event is called the first error
event and the corresponding probability is called the first error event probability. This
situation is depicted in Figure 10 .22.




A comparison of hard-decision decoding and soft-decision decoding for convolutional
codes shows that here, as in the case for linear block codes, soft-decision decoding
outperforms hard-decision decoding by a margin of roughly 2-3 dB in additive white
Gaussian noise channels.
Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis