CCS

Decoding of Convolutional Codes

Viterbi Algorithm

There exist many algorithms for decoding of convolutional codes. The Viterbi algorithm
is probably the most widely used decoding method for convolutional codes. This
algorithm is particularly interesting because it is a maximum-likelihood decoding algorithm,
which-upon receiving the channel output-searches through the trellis to find

the path that is most likely to have generated the received sequence. If hard-decision decoding
is used, this algorithm finds the path that is at the minimum Hamming distance
from the received sequence, and if soft-decision decoding is employed, the Viterbi algorithm
finds the path that is at the minimum Euclidean distance from the received sequence.

In hard-decision decoding of convolutional codes, we want to choose a path through
the trellis whose codeword, denoted by c, is at minimum Hamming distance from
the quantized received sequence y. In hard-decision decoding the channel is binary
memoryless (the fact that the channel is memoryless follows from the fact that the
channel noise is assumed to be white). Because the desired path starts from the all-0
state and returns back to the all-0 state, we assume that this path spans a total of m
branches, and because each branch corresponds to no bits of the encoder output, the
total number of bits inc and y is mno. We denote the sequence of bits corresponding
to the ith branch by Ci and Yi, respectively, where 1 :s: i :s: m and each Ci and Yi is of
length no. The Hamming distance between c andy is, therefore,

 

 

 

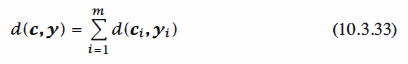
The preceding procedure can be summarized in the following algorithm, known as the Viterbi algorithm.

 

 

Matlab Coding

 

 

 

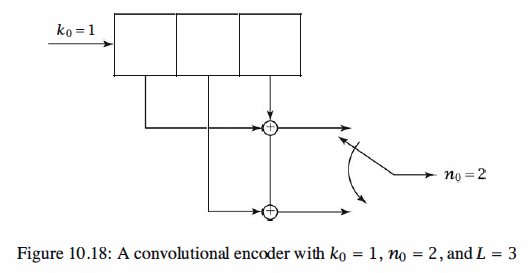
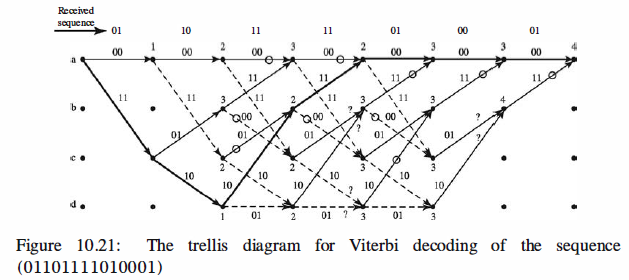
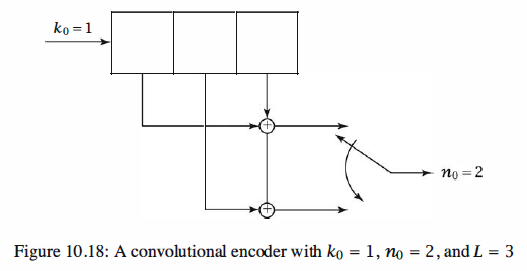
The path which is denoted by a heavy black line path through the trellis, is the optimal path. The
input-bit sequence corresponding to this path is 1100000, where the last two O's are
not information bits but were added to return the encoder to the all-0 state. Therefore,
the information sequence is 11000. The corresponding codeword for the selected path
is 11101011000000, which is at Hamming distance 4 from the received sequence. All
other paths through the trellis correspond to codewords that are at greater Hamming
distance from the received sequence.

For soft-decision decoding a similar procedure is followed, with squared Euclidean distances substituted for Hamming distances.

function [decoder_output,survivor_state,cumulated_metric]=viterbi(G,k,channel_output)
%VITERBI    The Viterbi decoder for convolutional codes
%        [decoder_output,survivor_state,cumulated_metric]=viterbi(G,k,channel_output)
%        G is a n x Lk matrix each row of which
%              determines the connections from the shift register to the
%              n-th output of the code, k/n is the rate of the code.
%              survivor_state is a matrix showing the optimal path through
%              the trellis. The metric is given in a separate function metric(x,y)
%              and can be specified to accommodate hard and soft decision.
%              This algorithm minimizes the metric rather than maximizing
%              the likelihood.
 
n=size(G,1);
%  check the sizes
if rem(size(G,2),k) ~=0 
  error('Size of G and k do not agree')
end
if rem(size(channel_output,2),n) ~=0
  error('channel output not of the right size')
end
L=size(G,2)/k;
number_of_states=2^((L-1)*k);
%  Generate state transition matrix, output matrix, and input matrix.
for j=0:number_of_states-1
  for l=0:2^k-1
    [next_state,memory_contents]=nxt_stat(j,l,L,k);
    input(j+1,next_state+1)=l;
    branch_output=rem(memory_contents*G',2);
    nextstate(j+1,l+1)=next_state;
    output(j+1,l+1)=bin2deci(branch_output);
  end
end
state_metric=zeros(number_of_states,2);
depth_of_trellis=length(channel_output)/n;
channel_output_matrix=reshape(channel_output,n,depth_of_trellis);
survivor_state=zeros(number_of_states,depth_of_trellis+1);
%  Start decoding of non-tail channel outputs.
for i=1:depth_of_trellis-L+1
  flag=zeros(1,number_of_states);
  if i <= L
    step=2^((L-i)*k);
  else
    step=1;
  end
  for j=0:step:number_of_states-1
    for l=0:2^k-1
      branch_metric=0;
      binary_output=deci2bin(output(j+1,l+1),n);
      for ll=1:n
        branch_metric=branch_metric+metric(channel_output_matrix(ll,i),binary_output(ll));
      end
      if((state_metric(nextstate(j+1,l+1)+1,2) > state_metric(j+1,1)...
        +branch_metric) | flag(nextstate(j+1,l+1)+1)==0)
        state_metric(nextstate(j+1,l+1)+1,2) = state_metric(j+1,1)+branch_metric;
        survivor_state(nextstate(j+1,l+1)+1,i+1)=j;
        flag(nextstate(j+1,l+1)+1)=1;
      end
    end
  end
  state_metric=state_metric(:,2:-1:1);
end
%  Start decoding of the tail channel-outputs.
for i=depth_of_trellis-L+2:depth_of_trellis
  flag=zeros(1,number_of_states);
  last_stop=number_of_states/(2^((i-depth_of_trellis+L-2)*k));
  for j=0:last_stop-1
      branch_metric=0;
      binary_output=deci2bin(output(j+1,1),n);
      for ll=1:n
        branch_metric=branch_metric+metric(channel_output_matrix(ll,i),binary_output(ll));
      end
      if((state_metric(nextstate(j+1,1)+1,2) > state_metric(j+1,1)...
        +branch_metric) | flag(nextstate(j+1,1)+1)==0)
        state_metric(nextstate(j+1,1)+1,2) = state_metric(j+1,1)+branch_metric;
        survivor_state(nextstate(j+1,1)+1,i+1)=j;
        flag(nextstate(j+1,1)+1)=1;
      end
  end
  state_metric=state_metric(:,2:-1:1);
end
%  Generate the decoder output from the optimal path.
state_sequence=zeros(1,depth_of_trellis+1);
state_sequence(1,depth_of_trellis)=survivor_state(1,depth_of_trellis+1);
for i=1:depth_of_trellis
  state_sequence(1,depth_of_trellis-i+1)=survivor_state((state_sequence(1,depth_of_trellis+2-i)...
  +1),depth_of_trellis-i+2);
end
decodeder_output_matrix=zeros(k,depth_of_trellis-L+1);
for i=1:depth_of_trellis-L+1
  dec_output_deci=input(state_sequence(1,i)+1,state_sequence(1,i+1)+1);
  dec_output_bin=deci2bin(dec_output_deci,k);
  decoder_output_matrix(:,i)=dec_output_bin(k:-1:1)';
end
decoder_output=reshape(decoder_output_matrix,1,k*(depth_of_trellis-L+1));
cumulated_metric=state_metric(1,1);


function distance=metric(x,y)
if x==y
  distance=0;
else
  distance=1;
end

Reference,

　　1. <<Contemporary Communication System using MATLAB>> - John G. Proakis