Performance of Linear Block Codes
Linear block codes can be decoded using either soft-decision decoding or hard-decision
decoding. In a hard-decision decoding scheme, first a bit-by-bit decision is made on the
components of the codeword, and then, with a minimum Hamming distance criterion,
the decoding is performed. The performance of this decoding scheme depends on the
distance structure of the code, but a tight upper bound, particularly at high values of
the SNR, can be obtained in terms of the minimum distance of the code.




Matlab Coding


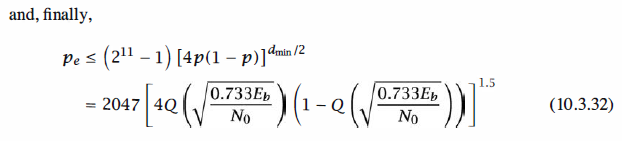
1 % MATLAB script for Illustrative Problem 10.11. 2 echo on 3 gamma_b_db=[-4:1:14]; 4 gamma_b=10.^(gamma_b_db/10); 5 qq=q(sqrt(0.733.*gamma_b)); 6 p_err=2047*qq.^2.*(3-2.*qq); 7 semilogy(gamma_b,p_err) 8 ylabel('Pe') 9 xlabel('dB')
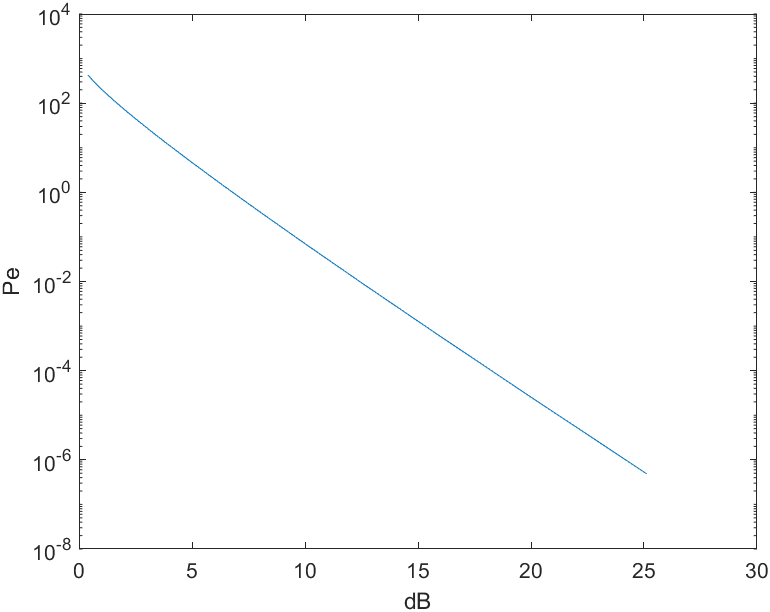



In comparing these error rate expressions, we observe that
antipodal signaling is 3 dB better than orthogonal signaling.
1 % MATLAB script for Illustrative Problem 10.12. 2 [p_err_ha,gamma_b]=p_e_hd_a(7,13,11,15,3); 3 [p_err_ho,gamma_b]=p_e_hd_o(7,13,11,15,3); 4 [p_err_so,gamma_b]=p_e_sd_o(7,13,11,15,3); 5 [p_err_sa,gamma_b]=p_e_sd_a(7,13,11,15,3); 6 semilogy(gamma_b,p_err_sa,gamma_b,p_err_so,gamma_b,p_err_ha,gamma_b,p_err_ho) 7 8 9 10 function [p_err,gamma_db]=p_e_sd_o(gamma_db_l,gamma_db_h,k,n,d_min) 11 % p_e_sd_o.m Matlab function for computing error probability in 12 % soft-decision decoding of a linear block code 13 % when orthogonal signaling is used. 14 % [p_err,gamma_db]=p_e_sd_o(gamma_db_l,gamma_db_h,k,n,d_min) 15 % gamma_db_l=lower E_b/N_0 16 % gamma_db_h=higher E_b/N_0 17 % k=number of information bits in the code 18 % n=code block length 19 % d_min=minimum distance of the code 20 21 gamma_db=[gamma_db_l:(gamma_db_h-gamma_db_l)/20:gamma_db_h]; 22 gamma_b=10.^(gamma_db/10); 23 R_c=k/n; 24 p_err=(2^k-1).*q(sqrt(d_min.*R_c.*gamma_b)); 25 26 27 28 function [p_err,gamma_db]=p_e_hd_o(gamma_db_l,gamma_db_h,k,n,d_min) 29 % p_e_hd_o.m Matlab function for computing error probability in 30 % hard-decision decoding of a linear block code 31 % when orthogonal signaling is used. 32 % [p_err,gamma_db]=p_e_hd_o(gamma_db_l,gamma_db_h,k,n,d_min) 33 % gamma_db_l=lower E_b/N_0 34 % gamma_db_h=higher E_b/N_0 35 % k=number of information bits in the code 36 % n=code block length 37 % d_min=minimum distance of the code 38 39 gamma_db=[gamma_db_l:(gamma_db_h-gamma_db_l)/20:gamma_db_h]; 40 gamma_b=10.^(gamma_db/10); 41 R_c=k/n; 42 p_b=q(sqrt(R_c.*gamma_b)); 43 p_err=(2^k-1).*(4*p_b.*(1-p_b)).^(d_min/2);
Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis