Matched Filter
The matched filter provides an alternative to the signal correlator for demodulating
the received signal r(t). A filter that is matched to the signal waveform s(t), where
0 <= t <= Tb, has an impulse response,


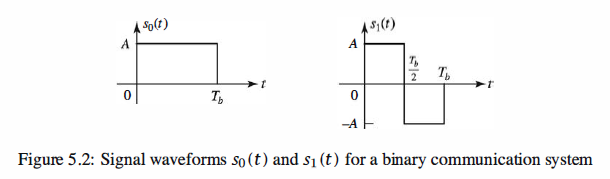

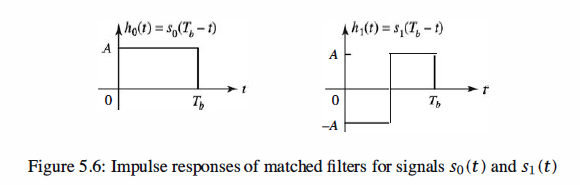
Note, Si(Tb - t) equals to the actions of folding Si(t) to get Si(-t) then delay it Tb( to the right, since Tb > 0) to obtain Si(Tb - t) .

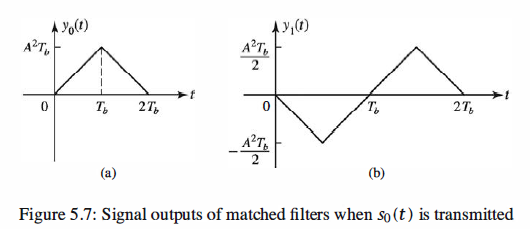


Matlab Coding
1 % MATLAB script 2 3 % Initialization: 4 K=20; % Number of samples 5 A=1; % Signal amplitude 6 l=0:K;
7 % Defining signal waveforms: 8 s_0=A*ones(1,K); 9 s_1=[A*ones(1,K/2) -A*ones(1,K/2)];
10 % Initializing output signals: 11 y_0=zeros(1,K); 12 y_1=zeros(1,K); 13 14 % Case 1: noise~N(0,0) 15 noise=random('Normal',0,0,1,K); 16 % Sub-case s = s_0: 17 s=s_0; 18 y=s+noise; % received signal 19 y_0=conv(y,wrev(s_0)); % Matched Filter 20 y_1=conv(y,wrev(s_1)); % Matched Filter
21 % Plotting the results: 22 subplot(3,2,1) 23 plot(l,[0 y_0(1:K)],'-k',l,[0 y_1(1:K)],'--k') 24 set(gca,'XTickLabel',{'0','5Tb','10Tb','15Tb','20Tb'}) 25 axis([0 20 -30 30]) 26 xlabel('(a) sigma^2= 0 & S_{0} is transmitted','fontsize',10) 27 % Sub-case s = s_1: 28 s=s_1; 29 y=s+noise; % received signal 30 y_0=conv(y,wrev(s_0)); 31 y_1=conv(y,wrev(s_1)); 32 % Plotting the results: 33 subplot(3,2,2) 34 plot(l,[0 y_0(1:K)],'-k',l,[0 y_1(1:K)],'--k') 35 set(gca,'XTickLabel',{'0','5Tb','10Tb','15Tb','20Tb'}) 36 axis([0 20 -30 30]) 37 xlabel('(b) sigma^2= 0 & S_{1} is transmitted','fontsize',10)
38 % Case 2: noise~N(0,0.1) 39 noise=random('Normal',0,0.1,1,K); 40 % Sub-case s = s_0: 41 s=s_0; 42 y=s+noise; % received signal 43 y_0=conv(y,wrev(s_0)); 44 y_1=conv(y,wrev(s_1)); 45 % Plotting the results: 46 subplot(3,2,3) 47 plot(l,[0 y_0(1:K)],'-k',l,[0 y_1(1:K)],'--k') 48 set(gca,'XTickLabel',{'0','5Tb','10Tb','15Tb','20Tb'}) 49 axis([0 20 -30 30]) 50 xlabel('(c) sigma^2= 0.1 & S_{0} is transmitted','fontsize',10) 51 % Sub-case s = s_1: 52 s=s_1; 53 y=s+noise; % received signal 54 y_0=conv(y,wrev(s_0)); 55 y_1=conv(y,wrev(s_1)); 56 % Plotting the results: 57 subplot(3,2,4) 58 plot(l,[0 y_0(1:K)],'-k',l,[0 y_1(1:K)],'--k') 59 set(gca,'XTickLabel',{'0','5Tb','10Tb','15Tb','20Tb'}) 60 axis([0 20 -30 30]) 61 xlabel('(d) sigma^2= 0.1 & S_{1} is transmitted','fontsize',10)
62 % Case 3: noise~N(0,1) 63 noise=random('Normal',0,1,1,K); 64 % Sub-case s = s_0: 65 s=s_0; 66 y=s+noise; % received signal 67 y_0=conv(y,wrev(s_0)); 68 y_1=conv(y,wrev(s_1)); 69 % Plotting the results: 70 subplot(3,2,5) 71 plot(l,[0 y_0(1:K)],'-k',l,[0 y_1(1:K)],'--k') 72 set(gca,'XTickLabel',{'0','5Tb','10Tb','15Tb','20Tb'}) 73 axis([0 20 -30 30]) 74 xlabel('(e) sigma^2= 1 & S_{0} is transmitted','fontsize',10) 75 % Sub-case s = s_1: 76 s=s_1; 77 y=s+noise; % received signal 78 y_0=conv(y,wrev(s_0)); 79 y_1=conv(y,wrev(s_1)); 80 % Plotting the results: 81 subplot(3,2,6) 82 plot(l,[0 y_0(1:K)],'-k',l,[0 y_1(1:K)],'--k') 83 set(gca,'XTickLabel',{'0','5Tb','10Tb','15Tb','20Tb'}) 84 axis([0 20 -30 30]) 85 xlabel('(f) sigma^2= 1 & S_{1} is transmitted','fontsize',10)
Simulation Result
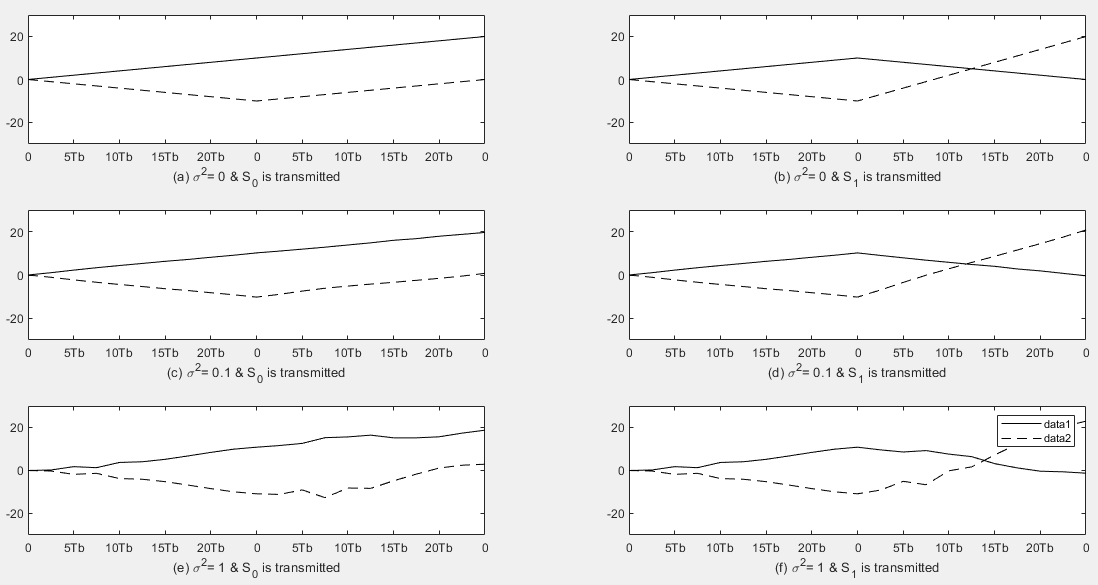
Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis